卡塔蘭數 Catalan Number

卡塔蘭數 (Catalan Number) 是組合數學中一個常在各種計數問題中出現的數列，數列的前幾項分別為：1, 1, 2, 5, 14, 42, 132, 429…

定義公式

$C_0 = 1, C_1 = 1$

一般項公式：

$C_n = \frac{1}{n+1}C_{n}^{2n} = C_{n}^{2n} - C_{n-1}^{2n}$

遞迴公式：

$C_{n+1} = \sum_{i=0}^{n}C_{i}C_{n-i}$
or
$C_{n} = \sum_{i=1}^{n}C_{i-1}C_{n-i}$

應用

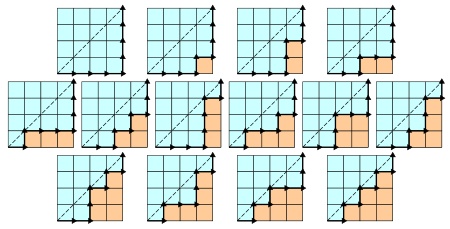
路徑問題

在一個 n * n 的格點中，從左下角 (0, 0) 到右上角 (n, n)，每一步只能向右或向上，不穿越對角線的總路徑數。

n = 4 的情形：

括號分配

有 a₁ , a₂ , …, a_n , a_n+1 ，共 n + 1 個數，中間用 n 個減號隔開，在式子中添加 n - 1 個括號，最後形成的排列數。
n = 3 的情形：
((a₁ - a₂) - a₃) - a₄
(a₁ - (a₂ - a₃)) - a₄
(a₁ - a₂) - (a₃ - a₄)
a₁ - ((a₂ - a₃) - a₄)
a₁ - (a₂ - (a₃ - a₄))

首先從 1 到 n 選定一個減號的位置 k，此時會將式子分為前後兩邊，前面有 k - 1 個減號，後面有 n - k 個減號，而前後也可以透過類似的方式計算，因此總排列數可以表達為 $f(n) = \sum_{k=1}^{n}f(k-1)f(n-k)$ 也就是卡塔蘭數的遞迴形式。

括號配對數

有 n 組括號，其中每組括號包含 “(” 以及 “)” ，所形成的合法排列數。
n = 3 的情形：
( ( ( ) ) )
( ( ) ( ) )
( ( ) ) ( )
( ) ( ( ) )
( ) ( ) ( )

假設第一個左括號所對應到的右括號位置在 k，此時該括號內包含 k - 1 對括號，外面有 n - k 對括號，而內外的括號排列也可以透過類似的方式計算，因此總排列數可以表達為 $f(n) = \sum_{k=1}^{n}f(k-1)f(n-k)$ 同樣也是卡塔蘭數的遞迴形式。

多邊形分割

有一個 n + 2 邊形，透過連接頂點，將其分割為 n 個三角形的所有可能 (旋轉視為相同分割法)。

首先選中其中一條邊，再選擇一個點之後就會形成一個三角形，共有 n 個頂點可以做選擇，假設選中了第 k 個點，此時三角形的左邊有 k + 1 個點，可以形成 k - 1 個三角形，右邊可以形成 n - k 個三角形，而左右的分割數也可以透過類似的方式計算，因此總分割數可以表達為 $f(n) = \sum_{k=1}^{n}f(k-1)f(n-k)$ 。

二元樹

一個二元樹有 n 個節點，其所有可能的結構。
n = 3 的情形 (月牙形代表空節點)：

將所有節點由 1 ~ n 進行排序，選中其中一點 k 作為根結點，該點左右兩邊分別為左右子樹，此時左子樹包含 k - 1 個節點，右子樹有 n - k 個節點，總排列數可以表達為 $f(n) = \sum_{k=1}^{n}f(k-1)f(n-k)$ 。