String

用於儲存字串的資料類型，內部為一個個的字元構成，可以進行很多類似陣列的操作，有以下幾個常見的操作：

  • size 回傳字串長度
  • [] 存取對應下標的字元
  • find 回傳指定字元的位置
  • substr 取出指定的子字串
  • reverse 反轉指定的字串

Stringstream

經常在操作字串時會使用到的類別，常用於類型轉換或是分割字串。

型態轉換

使用 stringstream

1
2
3
4
5
6
7
8
9
10
11
12
13
//int -> str
int i = 123;
string s;
stringstream ss;
ss << i;
ss >> s;

//str -> int
string s = "123";
int i;
stringstream ss;
ss << s;
ss >> i;

使用函數

1
2
3
4
5
6
7
8
9
//int -> str
int i = 123;
string s;
s = to_string(i);

//str -> int
string s = "123";
int i;
i = stoi(s);

分割字串

空白分割

1
2
3
4
5
6
7
8
9
10
11
12
string str = "Welcome to my blog", tmp;
stringstream ss(str);
while(ss >> tmp){
    cout << tmp << endl;
}

/*
Welcome
to
my
blog
*/

其他分割符

1
2
3
4
5
6
7
8
9
10
11
string str = "discuss.leetcode.com", tmp;
stringstream ss(str);
while (std::getline(ss, tmp, '.')) {
    cout << tmp << endl;
}

/*
discuss
leetcode
com
*/

字串匹配問題

給定一個主串 T 以及子串 p，在主串中尋找子串是否存在，以及其所在的位置。

樸素演算法

最容易想到的演算法，不需要進行預處理，從 T[0] 以及 p[0] 開始比較，如果相同就接著往下比較，如果出現相異的情況就退回到 T[1] 以及 p[0] 比較，直到主串的結尾。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int bruteForce(string T, string p) {
    int i = 0, j = 0;
    while(i < T.size() && j < p.size()){
        if(T[i] == p[j]){
            i++;
            j++;
        }else{
            i -= (j - 1);
            j = 0;
        }
    }
    if(j == p.size()) return i - j;
    else return -1;
}

這種演算法因為每次都要退回，效率較差，因此比較不推薦使用。

KMP 演算法

透過提前建立的 部分匹配表 可以在匹配失敗時利用失敗的資訊將子串的下標進行移動，進而繼續匹配，避免了之前的重複情形。

部分匹配表

通常會以 next 作為命名，其中每個位置 next[j] 的意義是子串 [0,j] 之間的最長相同前後綴，同時也是在之後 p[j + 1] 發生錯誤匹配時可以跳過檢查的長度。

範例：

i 0 1 2 3 4 5 6
p[j] A B C D A B D
next[j] 0 0 0 0 1 2 0
  • i = 4 時，“ABCDA” 有相同前後綴 “A”，長度為 1。
  • i = 5 時，“ABCDAB” 有相同前後綴 “AB”，長度為 2。
1
2
3
4
5
6
7
8
9
10
vector<int> buildNext(string p) {
    vector<int> next(p.size(), 0);
    int i = 1, len = 0;
    while(i < p.size()){
        if(p[i] == p[len]) next[i++] = ++len;
        else if(len) len = next[len - 1];
        else next[i++] = 0;
    }
    return next;
}

匹配原則

和樸素演算法一樣，從 T[0] 以及 p[0] 開始比較，如果相同就接著往下比較，不同的是在發生錯誤匹配時的處理，此時不用回退 i 的值，而是將 j 移到 next[j - 1] 對應的位置。因為我們知道相同前後綴的長度，因此就可以不用檢查對應的前綴長度，在不用回退的情況下執行至主串的結尾。

1
2
3
4
5
6
7
8
9
10
int KMP(string T, string p) {
    vector<int> next = buildNext(p);
    int j = 0;
    for(int i = 0; i < T.size(); i++){
        while(j > 0 && T[i] != p[j])  j = next[j - 1];
        if(T[i] == p[j]) j++;
        if(j == p.size()) return i - j + 1;
    }
    return -1;
}

BM 演算法

利用兩種規則來跳過無法匹配的情況，節省比較的時間，移動的方向是由左往右，但是匹配時的方向是從後方開始匹配。

  • 壞字符規則
    • 壞字符：匹配失敗時主字串的字符。
  • 好後綴規則
    • 好後綴：已經匹配成功的字串 (由後往前匹配，所以是後綴)。

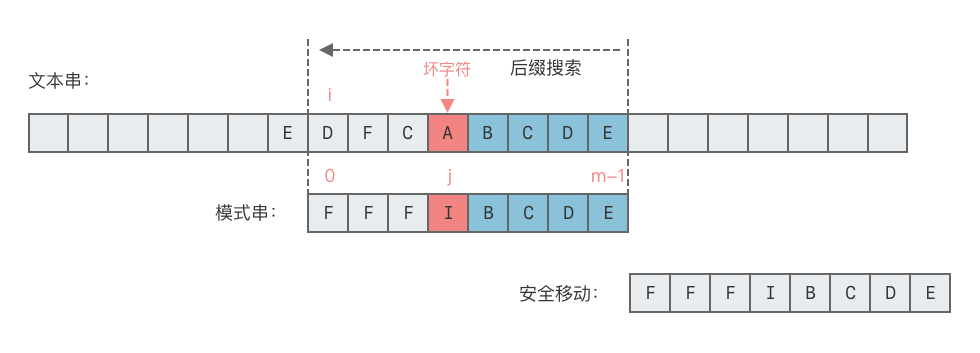
壞字符規則

  1. 匹配失敗時，將子串向右移動，使得主串的壞字符與子串中最右方的壞字符對齊，移動位數 = 子串的錯誤匹配位置 - 壞字符在子串中的最右位置。
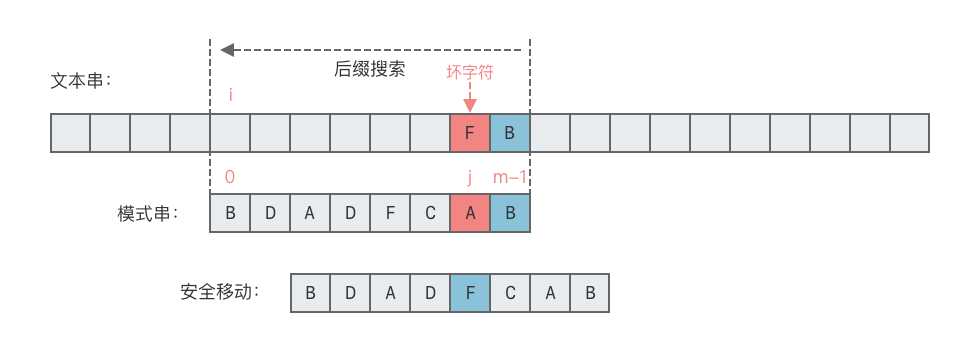
  1. 如果壞字符在子串中不存在，設定出現位置為 -1，即將整個子串右移 1 位。

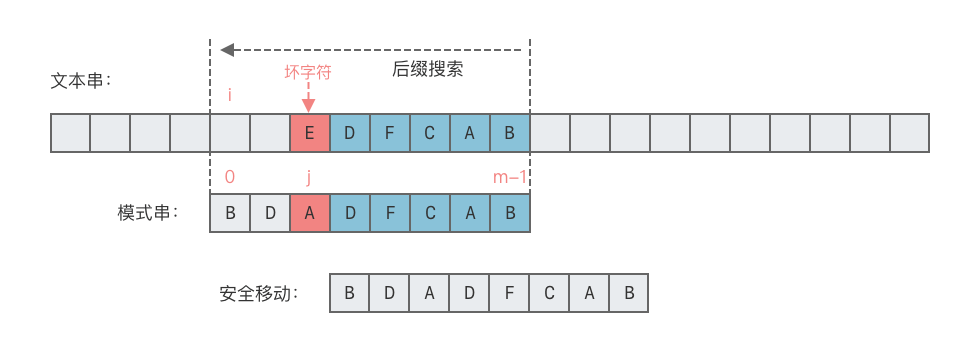
壞字符位置表 (紀錄每個字符出現的最右位置)：

1
2
3
4
5
6
7
unordered_map<int, int> buildBadCharTable(string p){
    unordered_map<int, int> badCharTable;
    for(int i = 0; i < p.size(); i++){
        badCharTable[p[i]] = i;
    }
    return badCharTable;
}

好後綴規則

  1. 找到子串中前一個好後綴出現的位置，將其與主串中的好後綴對齊，右移的位數 = 好後綴的位置 - 好後綴在子串中的上一個位置。
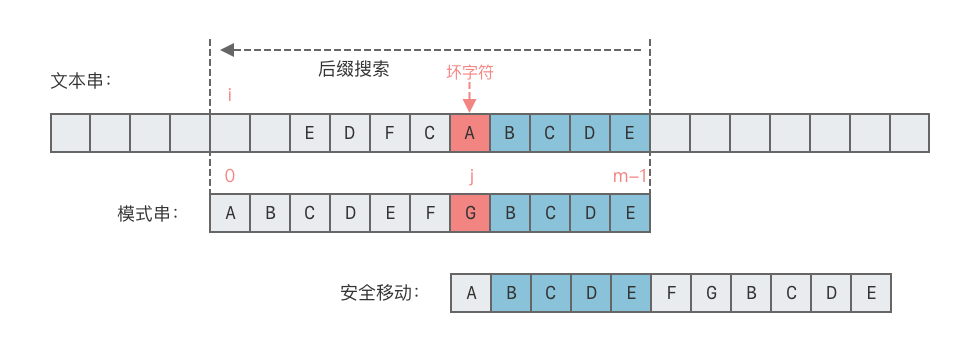
  1. 尋找子串中最長的相同前後綴 (子串的前綴 = 好後綴的後綴)，將兩者對齊，右移的位數 = 好後綴的位置 - 最長前綴的位置。
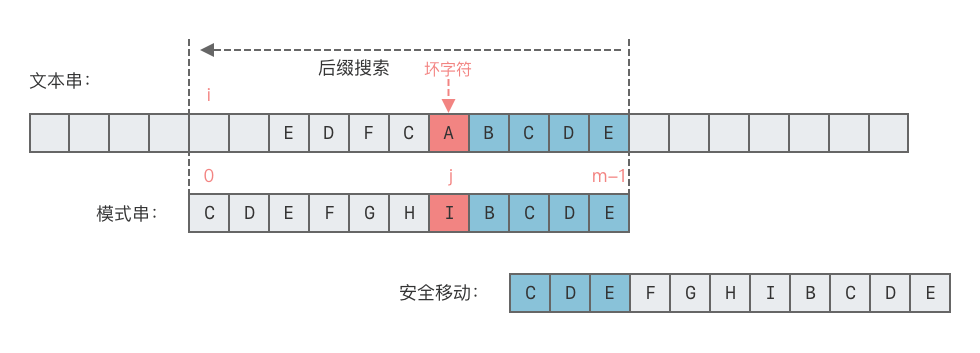
  1. 如果以上兩個條件都不存在，可以直接將整個子串右移，右移的位數 = 子串的長度。

定義一個後綴數組 suffix 儲存最大相同後綴的長度，每個值 suffix[i] 的意義是以下標 i 為結尾與子串匹配的最大相同後綴長。

1
2
3
4
5
6
7
8
9
vector<int> buildSuffix(string p){
    vector<int> suffix(p.size(), p.size());
    for(int i = p.size() - 2; i >= 0; i--){
        int start = i;
        while(start >= 0 && p[start] == p[p.size() - 1 - (i - start)]) start--;
        suffix[i] = i - start;
    }
    return suffix;
}

利用 suffix 數組，可以提前建立好後綴規則位移表，每個值 goodSuffixTable[j] 代表在下標 j 處遇到錯誤匹配時，根據好後綴規則所要右移的距離。

  • Type3
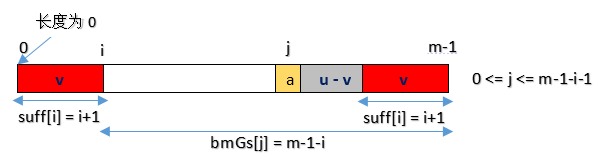
  • Type2
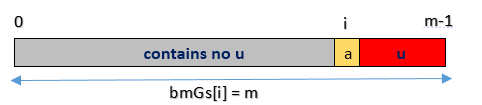
  • Type1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
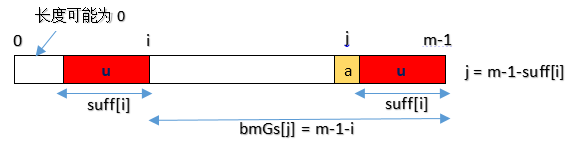
22
vector<int> buildGoodSuffixTable(string p){
    vector<int> goodSuffixTable(p.size(), p.size());
    //Type3
    vector<int> suffix = buildSuffix(p);
    int j = 0;
    //Type2 
    for(int i = p.size() - 1; i >= 0; i--){
        //相同前後綴
        if(suffix[i] == i + 1){
            while(j < p.size() - 1 - i){
                //好後綴的位置 - 最長前綴的位置
                if(goodSuffixTable[j] == p.size()) goodSuffixTable[j] = p.size() - 1 - i;
                j++;
            }
        }
    }
    //Type1
    for(int i = 0; i < p.size() - 2; i++){
        goodSuffixTable[p.size() - 1 - suffix[i]] = p.size() - 1 - i;
    }
    return goodSuffixTable;
}

如果同時有兩種情況成立，會選擇移動距離較小者，因此取值的順序是由 Type3、Type2 到 Type1。

合併使用

由主串的開頭開始，逐步將子串右移，每次從子串的後方開始比對，比對失敗時比較兩種規則產生的右移距離，取距離較大者進行移動，直到成功匹配為止。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int BM(string T, string p){
    if(T.size() < p.size()) return -1; //避免主串比子串短
    unordered_map<int, int> bcTable = buildBadCharTable(p);
    vector<int> gsTable = buildGoodSuffixTable(p);
    int i = 0;
    while(i <= T.size() - p.size()){
        int j = p.size() - 1; //由後往前匹配
        while(j >= 0 && T[i + j] == p[j]) j--;
        if(j < 0) return i; //成功匹配
        int bcMove = j - bcTable[T[i + j]];
        int gsMove = gsTable[j];
        i += max(bcMove, gsMove);
    }
    return -1;
}

內建 find 函數

1
size_t find (const char* s, size_t pos, size_t n) const;

<string> 內的 find 函數也可以在字串裡面尋找子串是否出現，如果有則會返回出現的位置，否則返回 string::npos，pos 為尋找的主串起始位置，n 為子串的匹配字元數 (前 n 位)。

1
2
3
size_t found = T.find(p);
if(found != std::string::npos) cout << found << endl;
else cout << -1 << endl;

練習

LeetCode 5. Longest Palindromic Substring

Given a string s, return the longest palindromic substring in s.

Example 1:
Input: s = “babad”
Output: “bab”

Example 2:
Input: s = “cbbd”
Output: “bb”

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    string longestPalindrome(string s) {
        vector<vector<bool>> v(s.size(), vector<bool>(s.size(), false));
        int ms, ml = 0;
        for(int i = 0; i < s.size(); i++){
            for(int j = 0; j <= i; j++){
                if(s[i] == s[j]){
                    if(i - j <= 2) v[i][j] = true;
                    else v[i][j] = v[i - 1][j + 1];
                }
                if(v[i][j] && i - j + 1 > ml){
                    ml = i - j + 1;
                    ms = j;
                }
            }
        }
        return s.substr(ms, ml);
    }
};

建立一個二維的陣列 v 儲存字串的每個子串是否是對稱的，當子串的開頭與結尾相同時：

  • 長度 <= 3：此子串必定對稱。
  • 長度 > 3：檢查去除頭尾的子串是否對稱。
    之後記錄下最長的對稱子串。

LeetCode 28. Find the Index of the First Occurrence in a String

Given two strings needle and haystack, return the index of the first occurrence of needle in haystack, or -1 if needle is not part of haystack.

Example 1:
Input: haystack = “sadbutsad”, needle = “sad”
Output: 0

Example 2:
Input: haystack = “leetcode”, needle = “leeto”
Output: -1

Solution:
使用前面的樸素演算法、KMP 演算法以及 BM 演算法都能通過，不過需要注意主串比子串短時有的演算法可能會有錯誤。

LeetCode 459. Repeated Substring Pattern

Given a string s, check if it can be constructed by taking a substring of it and appending multiple copies of the substring together.

Example 1:
Input: s = “abab”
Output: true

Example 2:
Input: s = “aba”
Output: false

Example 3:
Input: s = “abcabcabcabc”
Output: true

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    bool repeatedSubstringPattern(string s) {
        vector<int> next(s.size(), 0);
        int i = 1, len = 0;
        while(i < s.size()){
            if(s[i] == s[len]) next[i++] = ++len;
            else if(len) len = next[len - 1];
            else next[i++] = 0;
        }
        int l = next[s.size() - 1];
        return l > 0 && (s.size() % (s.size() - l) == 0);
    }
};

建立 KMP 算法中的 next 陣列，如果字串是由重複的子串構成，字串長度 - 最大相同前後綴長會是最小的重複子串長度，檢查字串長度是否為子串的整數倍即可。