演算法筆記-Tree-2

Binary Search Tree

二元搜尋樹有以下特性：

• 一個節點的左子樹只包含鍵值小於該節點的節點。
• 一個節點的右子樹只包含鍵值大於該節點的節點。
• 左子樹和右子樹也都是二分搜尋樹。
  而且以中序遍歷二元搜尋樹會得到一個遞增的數列。

操作

搜索

根據待查元素val 與當前 root -> val 的關係判斷：

• root -> val == val 回傳當前 root。
• root -> val > val 查找左子樹。
• root -> val < val 查找右子樹。

TreeNode* searchBST(TreeNode* root, int val) {
    if(root == nullptr) return nullptr;
    if(root -> val == val) return root;
    else if(root -> val > val) return searchBST(root -> left, val);
    else return searchBST(root -> right, val);
}

插入

根據待查元素val 與當前 root -> val 的關係判斷：

• root == nullptr 插入新節點。
• root -> val > val 重新構造左子樹。
• root -> val < val 重新構造右子樹。

TreeNode* insertIntoBST(TreeNode* root, int val) {
    if(root == nullptr) return new TreeNode(val);
    if(root -> val > val) root -> left = insertIntoBST(root -> left, val);
    else root -> right = insertIntoBST(root -> right, val);
    return root;
}

刪除

先用遞迴的方式找到要刪除的節點，並根據其左右子樹的情況做處理：

• 左右子樹皆為空：直接刪除節點，回傳 nullptr。
• 左子樹為空：以右子樹取代該節點，回傳 root -> right。
• 右子樹為空：以左子樹取代該節點，回傳 root -> left。
• 左右子樹皆不為空：把左子樹插入右子樹最小的節點的左邊，以右子樹取代該節點，回傳 root -> right。

TreeNode* deleteNode(TreeNode* root, int key) {
    if(root == nullptr) return nullptr;
    if(root -> val > key) root -> left = deleteNode(root -> left, key);
    else if(root -> val < key) root -> right = deleteNode(root -> right, key);
    else{
        if(root -> left == nullptr && root -> right == nullptr) return nullptr;
        if(root -> left == nullptr) return root -> right;
        else if(root -> right == nullptr) return root -> left;
        else{
            TreeNode* tmp = root -> right;
            while(tmp -> left != nullptr) tmp = tmp -> left;
            tmp -> left = root -> left;
            return root -> right;
        }
    }
    return root;
}

還原

前序

因為二元搜尋樹的特性，在區分左、右子樹時不需要利用到中序遍歷，只要在前序遍歷中找到鍵值大於根結點的地方就是右子樹。

TreeNode* buildTree(vector<int> preorder, int left, int right) {
    if (left > right) return nullptr;
    int preord_root = left;
    int size_left_subtree = 0;
    //找到右子樹在前序遍歷中的位置
    for(int i = left+1; i <= right; i++){
        if(preorder[i] > preorder[preord_root]) break;
        size_left_subtree++;
    }
    TreeNode* root = new TreeNode(preorder[preord_root], buildTree(preorder, left + 1, left + size_left_subtree), buildTree(preorder, left + size_left_subtree + 1, right));
    return root;
}

後序

和前序遍歷類似，只是根節點的位置要從最後面找。

中序

因為無法確定根結點所在的位置 (一定為遞增數列)，因此無法構造出唯一的樹。

Segment Tree

線段樹是二元平衡樹的一種，用以儲存區間或線段，每個節點代表一個區間，而根結點代表區間的全部範圍，葉節點代表長度為 1 的區間，而編號方式以及代表的區間規則如下：

• 根結點編號為 0，並且代表整個區間的範圍。
• 假設當前節點編號為 i，代表的區間為 [left, right]，假設 mid = (left + right) / 2 則：
  • 左節點編號為 i * 2，代表的區間為 [left, mid]。
  • 右節點編號為 i * 2 + 1，代表的區間為 [mid + 1, right]。

構造

假設有一數組 v，要建構一個線段樹來儲存每個區間的數字和，我們利用 tree 來儲存該線段樹的資料，建構的方式是使用遞迴不斷建立左右子節點，直到長度為 1 的葉節點。

vector<int> tree;
vector<int> v;
void build(int node, int left, int right){
    if(left == right) tree[node] = v[left];
    else{
        int mid = (left + right) / 2;
        build(node * 2, left, mid);
        build(node * 2 + 1, mid + 1, right);
        // 下面這一行可以替換為其他規則，建立不同的線段樹
        tree[node] = tree[node * 2] + tree[node * 2 + 1];
    }
    return;
}

查詢

查詢的過程依舊是由上而下進行遞迴，根據查詢的區間 [q_left, q_right] 以及結點所儲存的資料區間 [left, mid]，來決定回傳的結果，可以分為三種情況：

• 查詢區間和節點區間沒有交集，則回傳 0。
• 查詢區間包含節點區間，則回傳節點的值。
• 查詢區間與節點區間有部分交集，則分別對左右子樹進行查詢，接著將結果進行聚合 (聚合的方式視線段樹的規則而訂)。

int query(int node, int left, int right, int q_left, int q_right){
    if(q_right < left || q_left > right) return 0;
    if(q_left <= left && q_right >= right) return tree[node];
    int mid = (left + right) / 2;
    int res_left = query(node * 2, left, mid, q_left, q_right);
    int res_right = query(node * 2 + 1, mid + 1, right, q_left, q_right)
    // 下面這一行可以替換為其他規則，建立不同的線段樹
    return res_left + res_right;
}

更新

由上而下遞迴進行更新，不斷更新節點儲存的值，並且對子樹也進行更新，直到目標節點時才停止。

void update(int node, int left, int right, int index, int val){
    if(left == right){
        tree[node] = val;
        v[left] = val;
    }else{
        int mid = (left + right) / 2;
        if(index <= mid) update(node * 2, left, mid, index, val);
        else update(node * 2 + 1, mid + 1, right, index, val);
        // 下面這一行可以替換為其他規則，建立不同的線段樹
        tree[node] = tree[node * 2] + tree[node * 2 + 1];
    }
    return;
}

Disjoint set & Union-find algorithm

並查集是一種資料結構，用於處理一些不交集的合併及查詢問題，而使用的 Union-find algorithm 主要包含了以下功能：

• 查找 (Find)：查詢元素屬於哪個集合。
• 合併 (Union)：將兩個集合合併為一個。
  使用樹的概念儲存每個集合，樹的根結點就用來代表該集合，而所有樹所形成的森林則是所有的元素。

查找

因為樹的根結點代表該集合，因此在查找的時候只要不斷往回推，直到該節點指向自己 (根節點) 就好。

int Find(int x){
    if(p[x] == x) return x;
    return Find(p[x]);
}

合併

合併兩個集合其實就是把兩棵樹接起來，首先要先判斷各自的根結點，如果根結點相同則代表是相同集合，否則則要進行合併，將一個集合的根結點指向另一個集合的根結點即可。

void Union(int a,int b){
    int f1 = Find(a);
    int f2 = Find(b);
    if(f1 != f2) p[f2] = f1;
}

優化

路徑壓縮

經過路徑壓縮後，可以減少回推根結點時的迭代次數，增加效率，通常在查詢時順便進行壓縮。

int Find(int x){
    if(p[x] == x) return x;
    return p[x] = Find(p[x]); //把元素指向根結點
}

按秩合併

每次進行合併時，把秩比較小的樹根結點指向秩較大的樹根結點，秩主要有兩種定義方式，分別是樹的深度以及元素個數。

練習

LeetCode 110. Balanced Binary Tree

Given a binary tree, determine if it is height-balanced.

Example 1:

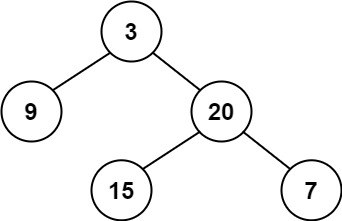
Input: root = [3,9,20,null,null,15,7]
Output: true

Example 2:

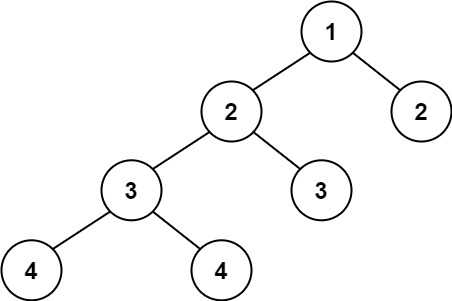
Input: root = [1,2,2,3,3,null,null,4,4]
Output: false

Example 3:
Input: root = []
Output: true

Solution:

class Solution {
public:
    int treeHeight(TreeNode* root){
        if(root == nullptr) return 0;
        int l = treeHeight(root -> left), r = treeHeight(root -> right);
        if(l == -1 || r == -1 || abs(l - r) > 1) return -1;
        return max(l, r) + 1;
    }
    bool isBalanced(TreeNode* root) {
        return treeHeight(root) != -1;
    }
};

建立一個 treeHeight 函數，在所在子樹為平衡二元樹時回傳其高度，否則回傳 -1，因此最終只要傳入根結點並判斷其回傳值是否為 -1 就好。

LeetCode 307. Range Sum Query - Mutable

Given an integer array nums, handle multiple queries of the following types:

1. Update the value of an element in nums.
2. Calculate the sum of the elements of nums between indices left and right inclusive where left <= right.

Implement the NumArray class:

• NumArray(int[] nums) Initializes the object with the integer array nums.
• void update(int index, int val) Updates the value of nums[index] to be val.
• int sumRange(int left, int right) Returns the sum of the elements of nums between indices left and right inclusive (i.e. nums[left] + nums[left + 1] + ... + nums[right]).

Example 1:
Input
[“NumArray”, “sumRange”, “update”, “sumRange”]
[[[1, 3, 5]], [0, 2], [1, 2], [0, 2]]
Output
[null, 9, null, 8]

Solution:

class NumArray {
public:
    vector<int> tree;
    vector<int> v;
    void build(int node, int left, int right){
        if(left == right) tree[node] = v[left];
        else{
            int mid = (left + right) / 2;
            build(node * 2, left, mid);
            build(node * 2 + 1, mid + 1, right);
            tree[node] = tree[node * 2] + tree[node * 2 + 1];
        }
        return;
    }
    int query(int node, int left, int right, int q_left, int q_right){
        if(q_right < left || q_left > right) return 0;
        if(q_left <= left && q_right >= right) return tree[node];
        int mid = (left + right) / 2;
        return query(node * 2, left, mid, q_left, q_right) + query(node * 2 + 1, mid + 1, right, q_left, q_right);
    }
    void updateN(int node, int left, int right, int index, int val){
        if(left == right){
            tree[node] = val;
            v[left] = val;
        }else{
            int mid = (left + right) / 2;
            if(index <= mid) updateN(node * 2, left, mid, index, val);
            else updateN(node * 2 + 1, mid + 1, right, index, val);
            tree[node] = tree[node * 2] + tree[node * 2 + 1];
        }
        return;
    }
    NumArray(vector<int>& nums) {
       v = nums;
       tree.resize(nums.size() * 4);
       if(!nums.empty()) build(1, 0, nums.size() - 1);
    }
    
    void update(int index, int val) {
        if (!v.empty()) updateN(1, 0, v.size() - 1, index, val);
        return;
    }
    
    int sumRange(int left, int right) {
        if (v.empty()) return 0;
        return query(1, 0, v.size() - 1, left, right);
    }
};

利用線段樹的方式儲存各區間的數字和，使用構造、查詢、更新三個函數。

LeetCode 399. Evaluate Division

You are given an array of variable pairs equations and an array of real numbers values, where equations[i] = [Ai, Bi] and values[i] represent the equation Ai / Bi = values[i]. Each Ai or Bi is a string that represents a single variable.

You are also given some queries, where queries[j] = [Cj, Dj] represents the j^th query where you must find the answer for Cj / Dj = ?.

Return the answers to all queries. If a single answer cannot be determined, return -1.0.

Note: The input is always valid. You may assume that evaluating the queries will not result in division by zero and that there is no contradiction.

Note: The variables that do not occur in the list of equations are undefined, so the answer cannot be determined for them.

Example 1:
Input: equations = [[“a”,“b”],[“b”,“c”]], values = [2.0,3.0], queries = [[“a”,“c”],[“b”,“a”],[“a”,“e”],[“a”,“a”],[“x”,“x”]]
Output: [6.00000,0.50000,-1.00000,1.00000,-1.00000]

Example 2:
Input: equations = [[“a”,“b”],[“b”,“c”],[“bc”,“cd”]], values = [1.5,2.5,5.0], queries = [[“a”,“c”],[“c”,“b”],[“bc”,“cd”],[“cd”,“bc”]]
Output: [3.75000,0.40000,5.00000,0.20000]

Example 3:
Input: equations = [[“a”,“b”]], values = [0.5], queries = [[“a”,“b”],[“b”,“a”],[“a”,“c”],[“x”,“y”]]
Output: [0.50000,2.00000,-1.00000,-1.00000]

Solution:

class Solution {
public:
    unordered_map<string, string> p;
    unordered_map<string, double> t;
    string Find(string s){
        while(s != p[s]) s = p[s];
        return s;
    }
    double FindTimes(string s){
        double ti = 1;
        while(s != p[s]){
            ti *= t[s];
            s = p[s];
        }
        return ti;
    }
    void Union(string x, string y, double ti){
        if(!p.count(x)){
            p[x] = x;
            t[x] = 1;
        }
        if(!p.count(y)){
            p[y] = y;
            t[y] = 1;
        }
        string f1 = Find(x), f2 = Find(y);
        if(f1 == f2) return;
        t[f2] = ti * FindTimes(x) / FindTimes(y);
        p[f2] = f1;
    }
    vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
        vector<double> ans;
        for(int i = 0; i < equations.size(); i++){
            Union(equations[i][0], equations[i][1], values[i]);
        }
        for(int i = 0; i < queries.size(); i++){
            if(p.count(queries[i][0]) == 0 || p.count(queries[i][1]) == 0) ans.push_back(-1);
            else if(Find(queries[i][0]) != Find(queries[i][1])) ans.push_back(-1);
            else{
                ans.push_back(FindTimes(queries[i][1]) / FindTimes(queries[i][0]));
            }
        }
        return ans;
    }
};

使用並查集以及一個 unordered map 來儲存變數之間的關係以及倍數，FindTimes 函數則是往回推算該變數與其根結點變數之間的倍數關係，在進行查詢時，可以分為幾種情況：

• 查詢變數不在並查集中：回傳 -1。
• 查詢變數不在相同的樹中 (根結點相異)：回傳 -1。
• 查詢變數在相同的樹中 (根結點相同)：回傳兩變數分別與根節點的倍數關係相除 FindTimes(queries[i][1]) / FindTimes(queries[i][0])。

LeetCode 765. Couples Holding Hands

There are n couples sitting in 2n seats arranged in a row and want to hold hands.

The people and seats are represented by an integer array row where row[i] is the ID of the person sitting in the i^th seat. The couples are numbered in order, the first couple being (0, 1), the second couple being (2, 3), and so on with the last couple being (2n - 2, 2n - 1).

Return the minimum number of swaps so that every couple is sitting side by side. A swap consists of choosing any two people, then they stand up and switch seats.

Example 1:
Input: row = [0,2,1,3]
Output: 1

Example 2:
Input: row = [3,2,0,1]
Output: 0

Solution:

class Solution {
public:
    vector<int> v;
    int Find(int x){
        if(v[x] == x) return x;
        return Find(v[x]);
    }
    void Union(int x, int y){
        int f1 = Find(x), f2 = Find(y);
        if(f1 == f2) return;
        v[f2] = f1;
    }
    int minSwapsCouples(vector<int>& row) {
        for(int i = 0; i < row.size() / 2; i++){
            v.push_back(i);
        }
        for(int i = 0; i < row.size(); i += 2){
            Union(row[i] / 2, row[i + 1] / 2);
        }
        for(int i = 0; i < v.size(); i++){
            v[i] = Find(i);
        }
        set<int> s(v.begin(), v.end());
        return v.size() - s.size();
    }
};

題解