Selection Sort

The Champion Problem

給定一個陣列，求出陣列中最小數字的下標。
Input: an array A of n integers.
Output: an index k so that A[k] is the minimum value in A.

Code:

int champion(int *s, int n){
    int ret = 0;
    for(int i=0; i<n; ++i){
        if(s[i] < s[ret]) ret = i;
    }
    return ret;
}

Sort

給定一個陣列，將其排序為遞增的陣列。
Input: an array A of n integers.
Output: the same array with the n integers ordered nondecrementally.

Code:

void selection_sort(int *s, int n){
    for(int i=0; i<n; ++i){
        int k = champion(s+i, n-i);
        int swap = s[i];
        s[i] = s[k];
        s[k] = swap;
    }
}

利用 champion 找出剩餘陣列中最小數字的下標，將其放到對應的位置。

Insertion Sort

Insert a number into a sorted array

將一個整數 x 插入一個已排序陣列 A 中，並且保持 A 是排序的狀態。
Input: a sorted array A of n integers and an integer x.
Output: a sorted array that comprises all elements in A and x.

Code:

void insert(int *s, int n, int x){
    bool placed = false;
    for(int i=n-1; i>=0 && !placed; --i){
        if(s[i] > x) s[i+1] = s[i];
        else{
            s[i+1] = x;
            placed = true;
        }
    }
    if(!placed) s[0] = x;
}

由後向前檢查合適的插入位置，如果到最後還沒有找到，則置於 s[0]。

Sort

給定一個陣列，將其排序為遞增的陣列。
Input: an array A of n integers.
Output: the same array with the n integers ordered nondecrementally.

Code:

void insertion_sort(int *s, int n){
    for(int i=1; i<n; ++i){
        insert(s, i, s[i]);
    }
}

由 s[1] 開始，依序將數字插入其前方已排序的陣列中。

Merge Sort

Merge two sorted arrays

將兩個已排序的陣列 A 和 B 合併為一個排序的陣列。
Input: two sorted arrays A and B of integers.
Output: a sorted array that comprises all elements in A and B.

Code:

int* merge(int *s, int n, int *r, int m){
    int *ret = new int [n+m];
    int i = 0, j = 0, k = 0;
    while( i < n || j < m ){
        if(i < n && j < m) ret[k++] = ((s[i] < r[j]) ? s[i++] : r[j++]);
        else ret[k++] = ((i < n) ? s[i++] : r[j++]);
    }
}

Sort

給定一個陣列，將其排序為遞增的陣列。
Input: an array A of n integers.
Output: the same array with the n integers ordered nondecrementally.

Code:

void merge_sort(int *s, int n){
    if(n == 1) return;
    int k = n/2;
    merge_sort(s, k);
    merge_sort(s+k, n-k);
    int *r = merge(s, k, s+k, n-k);
    memcpy(s, r, sizeof(int)*n);
}

利用遞迴的方式不斷將陣列分為兩部分進行排序，之後進行合併。

2D Sorted Arrays - Young Tableau

這裡要介紹的不是排序演算法，而是一個資料結構 Young Tableau (楊表)，Young Tableau 是一個 m * n 的矩陣，其特性是矩陣的每一行與列都是以遞增排序的 (由上而下、由左至右)，並且能在 O(m + n) 的時間複雜度下進行插入及查詢資料。

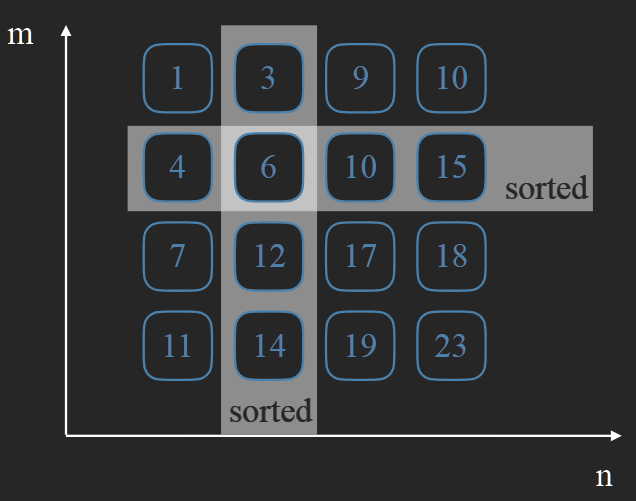
查詢

由二維陣列的右上角開始進行比對，每次與目標數字 x 比較有三種結果：

大於 x：將比對的格子向左移動，如果無法左移則結束。
等於 x：找到目標，結束。
小於 x：將比對的格子向下移動，如果無法下移則結束。

插入

將要插入的數字先放在二維陣列的右下角，檢查是否滿足 Young Tableau，如果不滿足則進行比較，每次比較其上方的數字 T 與左方的數字 L，如果該位置為空白則代表無限，比較有兩種結果：

L >= T：將插入的數字與 L 交換。
L < T：將插入的數字與 T 交換。
當滿足 Young Tableau 或是數字到達頂端或最左方時結束。

Heap Sort

Max-Heapify

調整指定的根結點與左右子結點，並且向下遞迴，使根結點為最大。
Max-Heapify(A, i)
convert the subtree rooted at node i into a max heap assuming that
(1) the subtree rooted at node Left(i) is a max heap, and
(2) the subtree rooted at node Right(i) is a max heap.

Build-Max-Heap

使指定的子樹滿足 Max Heap。
Convert the subtree rooted at node i into a max heap without the
assumption that heapification uses.

Code:

Build-Max-Heap(A, i){
    Build-Max-Heap(A, Left(i));
    Build-Max-Heap(A, Right(i));
    Max-Heapify(A, i);
}

Extract-Max

取出 Max Heap 裡面的最大值。
Extract-Max(A, n)
Remove the maximum from an n-element array A and keep the rest of A
as a max heap.

Code:

Extract-Max(A, int& n){
    int ret = A[1]; A[1] = -∞;
    Max-Heapify(A, 1);
    n --;
    return ret;
}

Sort

給定一個陣列，將其排序為遞增的陣列。
Input: an array A of n integers.
Output: the same array with the n integers ordered nondecrementally.

Code:

HeapSort(A, n){
    while(n > 1){
        k = Extract-Max(A, n);
        A[n+1] = k;
    }
}

不斷從 Max Heap 中取出最大值構成新的陣列。

Quick Sort

使用分治的方式進行排序，在陣列中選擇一個 pivot，並將陣列分成 小於等於 pivot 以及 大於 pivot 兩個部分，再以遞迴的方式接著處理兩個陣列，直到排序結束。

Sort

使用了長度為 n 的額外空間。

Code:

void QuickSort(int *A, int n, int *buf){
    int sfirst = 0, llast = n-1;
    int pivot = A[n-1];
    for(int i=0; i<n; ++i){
        if(A[i] ≤ pivot) buf[sfirst++] = A[i];
        else buf[llast--] = A[i];
    }
    memcpy(A, buf, sizeof(A[0])*n);
    QuickSort(A, sfirst, buf); QuickSort(A+sfirst, n-sfirst, buf);
}

In-Place Sort

不使用額外空間。

Code:

void QuickSort(int *A, int n){
    int slast = 0;
    int pivot = A[n-1];
    for(int i=0; i<n; ++i){
        if(A[i] ≤ pivot){
            int swap = A[i];
            A[i] = A[slast];
            A[slast++] = swap;
        }
    }
    QuickSort(A, slast); QuickSort(A+slast, n-slast);
}