考研相關文章參考資料為 wjungle 大神提供的筆記

Search

Linear Search

又稱為 Sequential Search，從頭到尾一一比較是否符合
特性:
- 不必事先進行排序
- 資料可以保存在 Ramdom Access (array) 或 Sequentail Access (link list) 結構中
時間複雜度: $O(n)$

Binary Search

預先準備
- 必須將資料排序 (小 -> 大)
- 資料必須保存在 Ramdom Access (array) 結構
可以做成 Iterative / Recursive 版本
時間複雜度: $O(\log n)$ $O (lo g n)$
- 最多比較次數為 Decision Tree (高度最小化的 BT) 之樹高

名詞區分

Worst case:
- Binary Search: $O(\log n)$
- Binary Search Tree: $O(n)$ (斜曲)

Sort

名詞解釋

Internal / External
- Internal: 資料量少，可以全部置於 memory 中進行排序
- External: 資料量大，無法全部置於 memory 中進行排序，需要藉助外部儲存體 (disk 等) 保存
  - merge sort (+ selection tree)
  - m-way search tree, B tree
Stable / Unstable
- 如果資料中存在多筆包含相同鍵值的資料，排序之後也能夠保持原本的前後關係，則此排序方式為 Stable，否則為 Unstable (存在不必要的 swap)

初等排序

平均時間複雜度為 $O(n^2)$

Insertion Sort

觀念: (迴圈)將第 i 筆資料插入到前面已排序的 i - 1 筆資料中的適當位置，形成 i 筆已排序資料
時間複雜度
- Best case: $O(n)$ (所有資料由小到大排好)
- Worst case: $O(n^2)$ (所有資料由大到小反序排列)
- Avg case: $O(n^2)$
空間複雜度: $O(1)$ (固定大小)
Stable

延伸: Binary / Linear Insertion Sort

Binary: 使用 Binary Search 找到資料的適當位置
Linear: 使用 link list 儲存資料，使插入元素時間減少
以下操作需要進行 n - 1 輪，兩種方法分別減少了尋找資料位置以及插入資料的時間，不過整體時間複雜度仍為 $O(n^2)$

	資料結構	決定資料位置	插入資料
Insertion Sort	Array	$O(n)$	$O(n)$
Binary Insertion Sort	Array	$O(\log n)$	$O(n)$
Linear Insertion Sort	Link list	$O(n)$	$O(1)$

Selection Sort

觀念: (迴圈)自第 i 筆至最後一筆資料中尋找最小值，並與第 i 筆資料進行 swap
時間複雜度
- Best / Worst / Avg case 皆為 $O(n^2)$
適合用於大型紀錄 (一筆資料包含多個欄位) 之排序上，因為每一回合最多進行一次 swap
空間複雜度: $O(1)$ (固定大小)
Unstable (交換時可能破壞順序)

Bubble Sort

觀念: (迴圈)由左而右，兩兩資料互相比較，如果前者 > 後者則進行 swap，每一回合會使最大值移動至最右邊
- 如果在某一回合沒有進行任何 swap 則可提前結束
也有由右往左進行比較的版本 (每回合將最小值移動至最左邊)
時間複雜度
- Best case: $O(n)$ (所有資料由小到大排好，第一輪沒有任何 swap)
- Worst case: $O(n^2)$ (所有資料由大到小反序排列)
- Avg case: $O(n^2)$
空間複雜度: $O(1)$ (固定大小)
Stable

Shell Sort

觀念: (迴圈)根據 span 將資料分為多組，在組內進行排序 (插入排序)，每組完成排序之後會縮小 span 的值，並再次進行排序，直到 span = 1 為止
span 型式:
- $\frac {n}{2^k}$ $\frac{n}{2 ^{k}}$ 型
  - ex: $\frac {n}{2}, \frac {n}{2^2},...,1$
- $2^k-1$ $2^{k} - 1$ 型
  - ex: $15,7,3,1$
- 自定型
時間複雜度
- Best case: $O(n^{1.5})$
- Worst case: $O(n^2)$
- Avg case: $O(n^2)$
空間複雜度: $O(1)$ (固定大小)
Unstable (分組排序時可能破壞順序)

高等排序

平均時間複雜度為 $O(\log n)$

Quick Sort

在 Avg case 下，實際執行時間最短的方法
採用 Divide and Conquer 策略
觀念: 令第一筆資料為 pivot key，經過處理後讓其位於正確位置 (左邊都比它小，右邊都比它大)，之後對於左右兩邊的 sublists 各自進行 Quick Sort

尋找正確位置

Hoare partition
- 建立 i, j 兩個指標分別位於左右兩端 (不包含 pivot key)
  * i 由左往右尋找比 >= pivot key 的值
  * j 由右往左尋找比 <= pivot key 小的值
- 當 i, j 都有找到目標，並且兩者尚未交會: 交換 i, j 所在位置的資料
- 當 i, j 交會 (j <= i)，則將 pivot key 與 j 所在位置的資料 swap
Lomuto Partition
- 建立 i, j 兩個指標皆位於最左方 (不包含 pivot key)
  - i 代表下一個比 pivot key 小的資料要放置的位置
  - j 由左往右尋找比 pivot key 小的資料
- 當 j 找到資料時，與 i 所在位置的資料 swap，並將 i++
- 遍歷結束後將 pivot key 與 i 所在位置的資料 swap

時間複雜度
- Best case: $O(n\log n)$ (pivot key 恰巧將資料分為兩等分)
- Worst case: $O(n^2)$ (pivot key 恰巧為最小/最大值，切割無效)
- Avg case: $O(n\log n)$

避免 Worst case

Middle of three
- 取要排序的資料的頭尾以及中間 (l + r / 2)
- 三者比較找出中間值，並將其與 l 交換作為 pivot key
Ramdomized Quick Sort
- 使用亂數挑選 pivot key
- Worst case 仍然為 $O(n^2)$
Median of medians (見最後的補充)

空間複雜度: 取決於 recursion 所需要的 stack space
- Best case: $O(\log n)$
- Worst case: $O(n)$
Unstable (交換時可能破壞順序)

Merge Sort

是 External sort 常用方法之一
名詞解釋:
- Run: 排序好的片段資料
- Run 長度: Run 中的資料個數
可分為 Iterative / Recursive 版本
- Iterative:
  - 將所有資料視為一個一個長度為 1 的 run
  - 由左而右兩個兩個 run 進行合併
  - 重複直到只剩下一個 run
- Recursive:
  - 採用 Divide and Conquer 策略
  - 將所有資料分為左右兩半，各自進行 Merge Sort
  - 將左右兩半排序完的資料進行合併
時間複雜度
- Best / Worst / Avg case 皆為 $O(n\log n)$
空間複雜度: $O(n)$
Stable

Selection Tree

用於 k-way merge (將 k 個 run 合併)，可加速尋找最小值的過程，時間複雜度為 $O(k)$

Winner tree
- 將每個 run 的最小值作為葉節點
- 由下而上兩兩比較選出較小者作為父節點，直到決定出 root
- 輸出最小值 (root)，並由該值來源的 run 中的值進行遞補 (與兄弟節點進行比較並調整父節點)
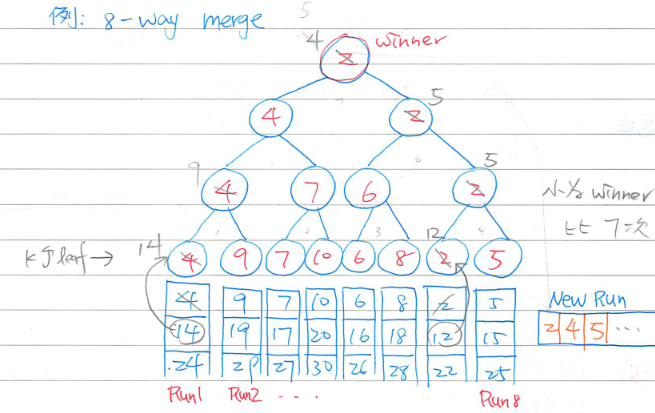
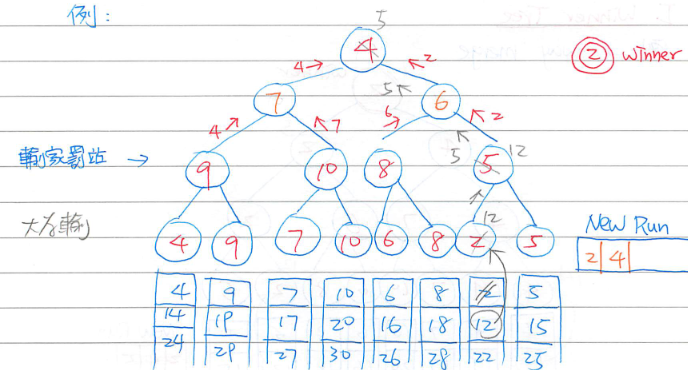
Loser tree (比較常用)
- 類似 winner tree，但是父節點的值為較大者 (輸家)
- 向上比較的仍然為兩者的較小值
- 遞補之後，每次比較時是與父節點進行比較
- 比較次數較少，因此較常被使用

Heap Sort

觀念:
- 先用 bottom up 方法建立 Max-heap
- (迴圈)執行類似 Delete-Max 的操作: 將 root 與 heap 中最後一個資料 swap，之後進行 heap 的調整 (heap 的大小會 -1)，直到 heap 中只剩下一個資料
時間複雜度
- Best / Worst / Avg case 皆為 $O(n\log n)$
空間複雜度: $O(1)$
Unstable (heap 調整時可能破壞順序)

比較

	操作輪數	每輪操作時間
Quick Sort	$O(\log n)$	$O(n)$
Merge Sort	$O(\log n)$	$O(n)$
Heap Sort	$O(n)$	$O(\log n)$

線性排序

不是採用 Comparison-based 的排序技巧，因此可以突破 $Ω(n\log n)$ ，達成線性時間 $O(n)$

Radix Sort

又稱為 Bin Sort, Bucket Sort
使用 Distribution & Merge (分派 & 合併) 的排序技巧
可分為 LSD / MSD Radix Sort

	DS 版本	Algo 版本
straight radix	LSD Radix Sort	Radix Sort
radix exchange	MSD Radix Sort	Bucket Sort

LSD Radix Sort

令 r 為採用之基底: Bucket 編號為 0 ~ (r - 1)
令 d 為資料中最大值的位數個數: 代表需要進行 d 回合
- 資料的範圍受到限制
由最低位數開始，往最高位數進行每回合的分派動作
每回合之操作 (d 回合):
- 分派: 根據該位數的數值，將資料放入對應的 Bucket 中
- 合併: 由 0 ~ (r - 1) 依序合併 Bucket 成一個串列
  - Bucket 中資料為 FIFO
時間複雜度: $O(n)$ $O (n)$ 等級
- $O(d*(n+r))$ $O (d * (n + r))$
  - 分派: $O(n)$
  - 合併: $O(r)$
空間複雜度: $O(n)$ $O (n)$ 等級
- $O(r*n)$
Stable

MSD Radix Sort

與 LSD 不同，只進行一次分派與合併
- 根據資料的最大位數，分配到各個 Bucket 中
- 每個 Bucket 內部各自進行排序
- 由 0 ~ (r - 1) 依序合併 Bucket 成一個串列
Stable (由 Bucket 內部的排序方式決定)
當 Bucket 數量足夠多，時間會接近線性 $O(n+k)$

Counting Sort

假設資料的範圍為 1 ~ k
觀念:
- 準備一個陣列統計各個鍵值的出現次數 Count[]
- 求出排序資料後各個鍵值的起始位置 Start[]
- 由左往右遍歷原始陣列，根據 Start[] 之指示，將鍵值 i 放到 Output array 中的 Start[i] 位置，並將 Start[i]++
時間複雜度: $O(n+k)$ $O (n + k)$
- 鍵值範圍 k 為 $O(n)$ 等級

鍵值範圍 k 的等級

如果鍵值範圍 k 為 $O(n^2)$ $O (n^{2})$ 等級，是否還是線性排序?
- 利用 LSD Radix Sort，進行兩回合:
  - pass 1: 以 $(Data_i \% n)$ 作為排序依據，進行 Counting Sort
  - pass 2: 以 $([Data_i/n] \% n)$ 作為排序依據，進行 Counting Sort
- 花了 $O(2n)$ 時間，仍為線性時間
$O(n^3),O(n^4),...$ 等級同理

統整

初等排序	Bset T	Avg T	Worst T	Space	Stable/Unstable
Insertion Sort	$O(n)$ `*`	$O(n^2)$	$O(n^2)$	$O(1)$	S
Selection Sort	$O(n^2)$	$O(n^2)$	$O(n^2)$	$O(1)$	U`*`
Bubble Sort	$O(n)$ `*`	$O(n^2)$	$O(n^2)$	$O(1)$	S
Shell Sort	$O(n^{1.5})$	$O(n^2)$	$O(n^2)$	$O(1)$	U`*`

高等排序	Bset T	Avg T	Worst T	Space	Stable/Unstable
Quick Sort	$O(n\log n)$	$O(n^2)$ `*`	$O(n\log n)$	$O(\log n)$ ~ $O(n)$	U`*`
Merge Sort	$O(n\log n)$	$O(n\log n)$	$O(n\log n)$	$O(n)$	S
Heap Sort	$O(n\log n)$	$O(n\log n)$	$O(n\log n)$	$O(1)$	U`*`

線性排序	Time	Space	Stable/Unstable
Radix Sort	$O(d*(n+r))$	$O(r*n)$	S
Counting Sort	$O(n+k)$	$O(n+k)$	S

補充-Selection Problem

如何在 n 個資料中，選出第 i 小的資料

方法一: 將資料排序後取出第 i 個
- 時間複雜度 $O(n\log n)$ (沒有限制資料範圍)
方法二: 利用 Quick Sort 中的 Partition 方法
- 利用 pivot key 將資料分為兩堆，並根據 pivot key 的位置 k 決定下一步
  - 如果 k < i: 搜尋右邊 subkist 第 i - k 小的資料
  - 如果 k > i: 搜尋右邊 subkist 第 i 小的資料
  - 如果 k = i: 回傳資料
- 時間複雜度
  - Best case: $O(n)$
  - Worst case: $O(n^2)$ (pivot key 恰巧為最小/最大值，切割無效)
  - Avg case: $O(n)$
方法三: Median of medians
- 操作:
  - 將所有資料每 5 個為一組進行分配，並且對每一個組內進行 Insertion Sort，挑選出中間值 (第三個)
  - 對所有組別的中間值利用 Selection 遞迴取出其中間值
  - 將 Median of medians 作為 pivot key 進行 Partition 取得位置 k
- 類用這個方法進行 Partition 的 Worst case 時間複雜度仍為 $O(n)$ $O (n)$
  - 證明見 wjungle 大神的筆記
- 分組時至少 5 個為一組，比 5 小則時間複雜度無法達到 $O(n)$