正規語言-L1
正規語言相關文章參考資料為陳穎平教授上課講義
Regular Languages
Finite Automata
有限自動機
or DFA: Deterministic finite automata 決定性有限自動機
Formal Definition of Finite Automata
DefinitionA finite automaton is a 5-tuple , where
- : is a finite set called the
states; - : is a finite set called the
alphabet; - : is the
transition function; - : is the
start state; - : is the set of
accept states or final states.
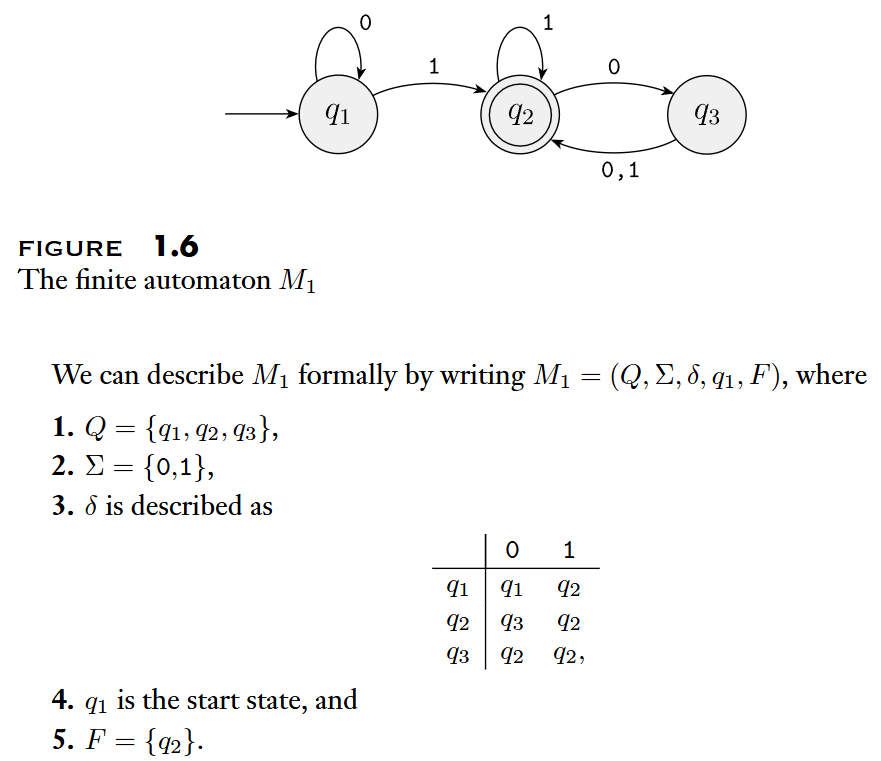
Formal Definition of Computation
Finite automaton accepts string if a sequence of states in exists with three conditions:
- ;
滿足起始狀態 - ;
滿足狀態轉移 - .
滿足結束狀態
A language is called a regular language if some finite automaton recognizes it.
The Regular Operations
DefinitionLet A and B be languages, let’s define the following three regular operations:
Union: ;Concatenation: ;Star: .
The class of regular languages is closed under the union/concatenation/Star operation.
Nondeterminism
NFA: Nondeterministic finite automata 非決定性有限自動機
Deterministiccomputation: Determined next move.Nondeterministiccomputation: Several choices may exist for the next move. (類似fork a process)
Formal Definition of NFAs
DefinitionA nondeterministic finite automaton is a 5-tuple , where
- : is a finite set of
states; - : is a finite
alphabet; - : is the
transition function; - ∈ Q: is the
start state; - : is the set of
accept states.

Formal Definition of Computation
Nondeterministic finite automaton accepts string , where , if a sequence of states in exists with three conditions:
- ;
- ;
- .
Equivalence of NFAs and DFAs
TheoremEvery DFA has an equivalent NFA.
- 容易證明 (DFA 是 NFA 的特例)
- 只需要修改
transition function
Every NFA has an equivalent DFA.
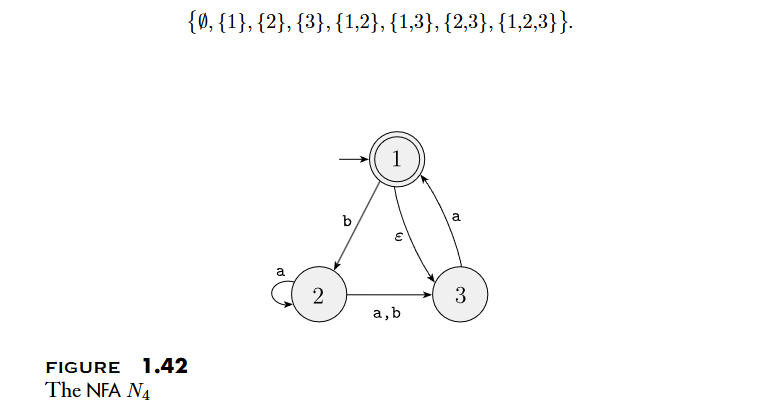
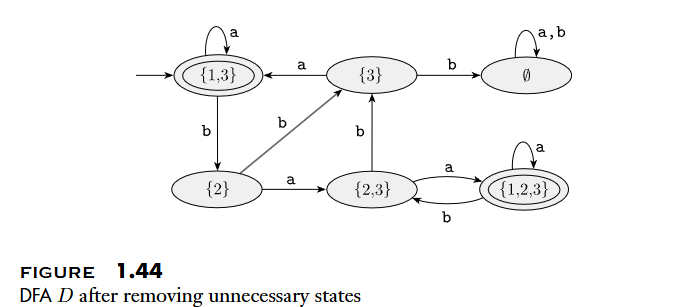
- 證明: 將一個 NFA: 改寫為 DFA:
-
- ex:
- 考慮加上 的情況
- 定義 : 經過 0 至多個 arrows 之後所能到達的狀態的集合

 Corollary
Corollary
A language is regular if and only if some nondeterministic finite automaton recognizes it.
Closure under the Regular Operations
根據以上性質,我們可以透過建立 NFA 的方式來證明 Regular Operations 的封閉性
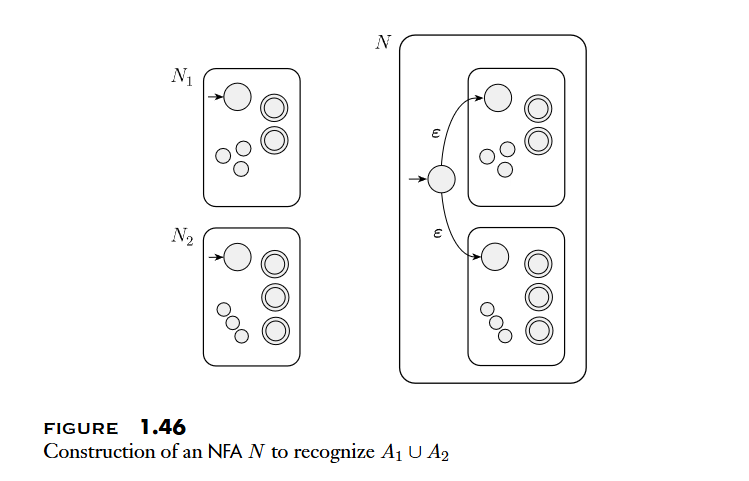
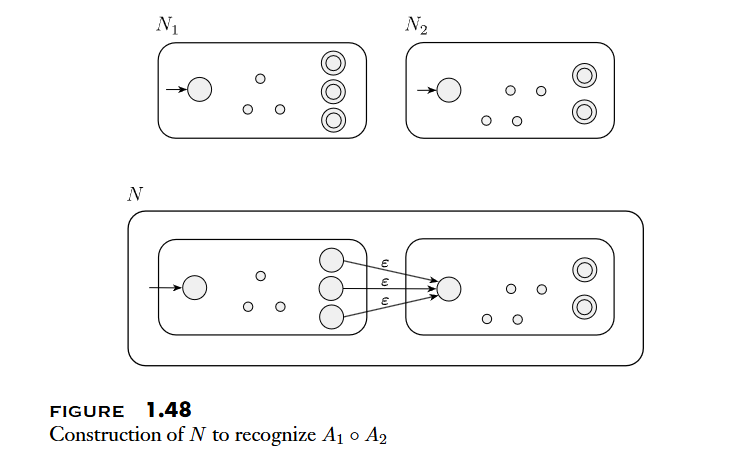
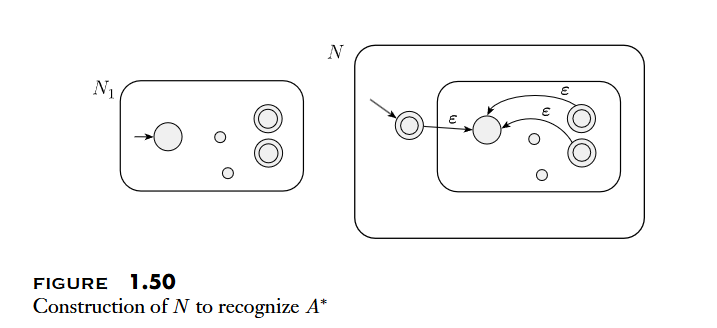
Regular Expressions
RE: 正則表達式 - 用於表達某個特定 language
Formal Definition (Inductive Definition)
Definition is a regular expression if is
- for some in the alphabet ;
包含 1 個長度為 1 的字串regular expression所表達的 language 是
- ;
包含 1 個長度為 0 的字串 - ;
包含 0 個字串 (空集合) - , where and are regular expressions
;類似加法 - , where and are regular expressions
;類似乘法 - , where is a regular expression .

Equivalence with Finite Automata
TheoremA language is regular if and only if some regular expression describes it.
If a language is described by a regular expression, then it is regular.
- 證明: Use an
NFAto recognize the language described by aregular expression.- 根據
regular expression的定義:- , then
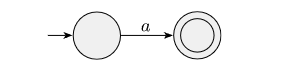
- , then

- , then
-
已經證過其封閉性 -
已經證過其封閉性 -
已經證過其封閉性
- , then
- 根據
 Lemma
Lemma
If a language is regular, then it is described by a regular expression.
- 證明: Convert
DFAsintoregular expressions.
首先定義 GNFA 幫助轉換:
A generalized nondeterministic finite automaton is a 5-tuple , where
- : is a finite set of
states; - : is the input
alphabet; - : is the
transition function; - : is the
start state; - : is the
accept state.唯一的接受狀態
A GNFA accepts a string in if , where each and a sequenceof states exists such that
- ;
- ;
- for each , we have , where .

- Every
DFAhas an equivalentGNFA.- 容易證明 (DFA 是 GNFA 的特例)
- 加上一個
start state,用 與原有的 連接 - 加上一個
accept state,用 與原有的 每個點連接 - 將原本
transition function的symbol改為regular expressions
CONVERT(G)是用來刪除節點的函式-
Claim
For any
GNFA,CONVERT(G)is equivalent to .
-
Claim
For any
- 將
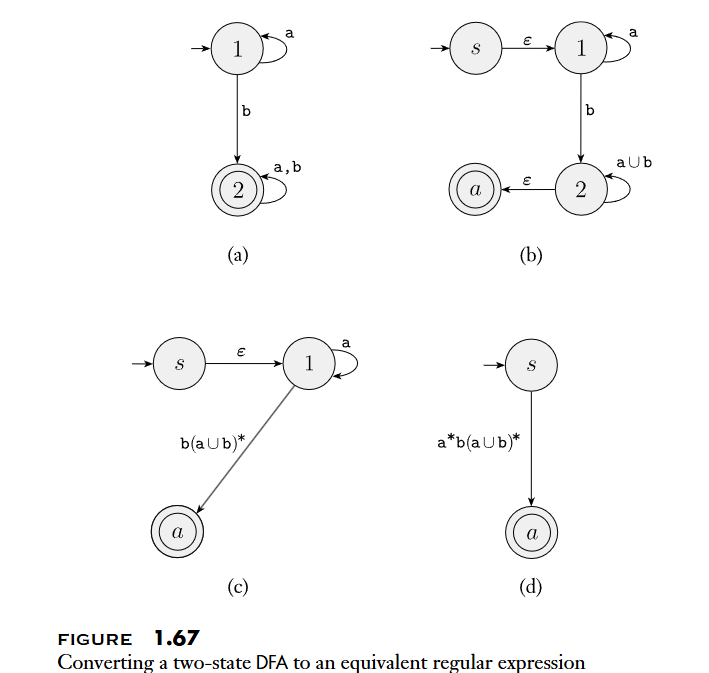
DFA轉為GNFA,之後利用CONVERT(G)不斷刪除節點,直到只剩下加上的start state和accept state時,兩者之間的就是其對應的regular expressions- 刪除節點的順序可能會影響最終的
regular expressions,但是他們描述的language是相同的
- 刪除節點的順序可能會影響最終的

Nonregular Languages
我們要如何去證明一個 Languages 是 Nonregular Languages 呢?
ex:
Pumping Lemma
TheoremIf is a regular language, then there is a number p (the pumping length) where, if is any string in of length at least , then may be divided into three pieces, , satisfying the following conditions:
- for each , ;
- ;
y 不為空字串 - .
在 p 範圍內一定會有重複

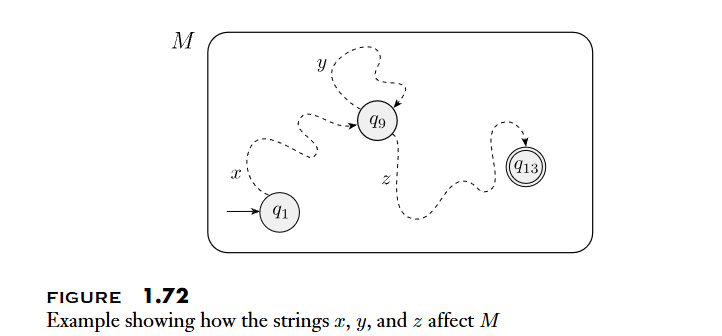
- 證明: 將 以
DFA表示,並且此DFA的states 數量為 p,如果一個 string 的長度大於p,則其至少需要經過p + 1 個 states,根據鴿籠原理必定有state是重複經過的,則重複的state之間那段就是y,可以對y進行Pumping且保持為regular language
有了 Pumping Lemma,我們可以利用反證法去證明一個 Languages 是 nonregular languages:
- Assume the language, say, , is
regularin order to obtain a contradiction. - By the
pumping lemma, a pumping lengthpexists, and any string can be pumped if . - Find a string , , that cannot be pumped as described in the pumping lemma.
尋找反例 - The
contradictionis obtained, and therefore, is proved to benonregular.

Closure Properties
Let and be regular languages. The results of the
following operations are all regular languages:
Union: ;Concatenation: ;Star: ;Intersection: ;Complement: (i.e., );- 證明: 將
DFA的accept states改為
- 證明: 將
Difference: ();Reversal: ;- 證明: 將原本的
DFA修改為NFA- 加上一個
start state,用 與原有的 每個點連接 - 加上一個
accept state,用 與原有的 連接 - 將原本
transition function的指向對調 (箭頭方向顛倒)
- 加上一個
- 證明: 將原本的
Homomorphism: ;- A
string substitutionsuch that each symbol is replaced by a single string. That is, . - 證明:
RE中的symbol經過替換之後會形成新的RE用於描述新產生的languages
- A
Inverse homomorphism: .- 所有會映射到 的 string 的集合
- .
- 證明: 根據在 上面的
DFA,以及 symbol 對應 string 的關係,可以建立一個在 上面的DFA
Myhill-Nerode Theorem
首先定義 indistinguishable 這個關係,主要可以用來將 string 分組:
Relation defined by a given language: Let and be strings and be any language. We say that and are distinguishable by if some string exists whereby exactly one of the strings and is a member of ;
otherwise, for every string , we have whenever and we say that and are indistinguishable by . If and are indistinguishable by we write . In other words, for , iff for each : .
is an equivlance relation because obviously
Reflexive: ;Symmetric: ;Transitive: .
Let be a language and let be a set of strings. Say that is pairwise distinguishable by if every two distinct strings in are distinguishable by . Define the index of L to be the maximum number of elements in any set that is pairwise distinguishable by . The index of L may be finite or infinite.
- If is recognized by a
DFAwith states, hasindexat most . - If the
indexof is a finite number , it is recognized by aDFAwith states. - is
regulariff it hasfinite index. Moreover, its index is the size of the smallestDFArecognizing it.
有了 Myhill-Nerode Theorem,我們可以證明一個 Languages 是 regular language 或是 nonregular languages:
- Given a langauge , construct the equivalence relation by using .
- Prove that has
finite or infinite index:
Finite: is aregular language.Infinite: is anonregular language.
Minimization of DFAs
根據 Myhill-Nerode Theorem 我們可以知道 index of L 是能夠 accept 的最小 DFA 的 states 數量,如果有一個 DFA 的 states 數量比 index of L 多,但是也能夠 accept ,這時這個 DFA 內部有一些 states 實際上是等價的,可以將其進行合併操作,使其最小化
Equivalent states: State and state are said to be
equivalent if for all , ; and distinguishable otherwise.
Table-filling Algorithm
Given DFA , the following algorithm finds all distinguishable pairs in .
- Basis: If and , is
distinguishable. - Induction step: If is
distinguishable, and , , for some , then isdistinguishable.
實際操作: 以一個 table (類似 queue 的功能) 來紀錄要檢查的 pair
- 先將
accept states與其餘 states 組成的 pairs 加上標示 (數字) - 從 table 中取出 pair,往前推前一步的
distinguishable pairs,並將其標上數字 - 重複直到 table 上有數字的 pair 都檢查過
- table 上沒有被標記過的 pair 即為
Equivalent states pairs

得到 Equivalent state pairs: , , and .
Equivalent states in a given DFA can be found by the table-filling algorithm, and therefore, the DFA can be minimized by combining each set of equivalent states into one single state.