正規語言相關文章參考資料為陳穎平教授上課講義

L2 Context-Free Languages

Context-Free Grammars

CFGs: 上下文無關文法，指的是字元在進行替換時不需要考慮上下文，其擁有足夠的表現力來表示大多數程式設計語言的語法

Formal Definition of CFGs

Definition

A context-free grammar is a 4-tuple $(V, Σ, R, S)$ , where

$V$ is a finite set called the variables;
$Σ$ is a finite set, disjoint from $V$ ,called the terminals;
$R$ is a finite set of rules (or productions), with each rule being a variable and a string of variables and terminals;
$S ∈ V$ is the start variable.

Each rule consists of

head: variable in $V$
symbol →
body: a string in $(V ∪ Σ)^∗$

If $u, v, w ∈ (V ∪ Σ)^∗$ , and $A → w$ is a rule of the grammar, we say that $uAv$ yields $uwv$ , written $uAv ⇒ uwv$ .
Say that $u$ derives $v$ , written $u ⇒^* v$ , if $u = v$ or if a sequence $u_1, u_2, ··· , u_k$ exists for $k ≥ 0$ and $u ⇒ u_1 ⇒ u_2 ⇒ ··· ⇒ v$ .
The language of the grammar is $\{w ∈ Σ^∗~|~S ⇒^* w\}$ .

Ambiguity

Leftmost derivation: A derivation of a string w in a grammar G is a leftmost derivation if at every step the leftmost remaining variable is the one replaced.

Definition

A string $w$ is derived ambiguously in context-free grammar $G$ if it has two or more different leftmost derivations. Grammar $G$ is ambiguous if it generates some string ambiguously.

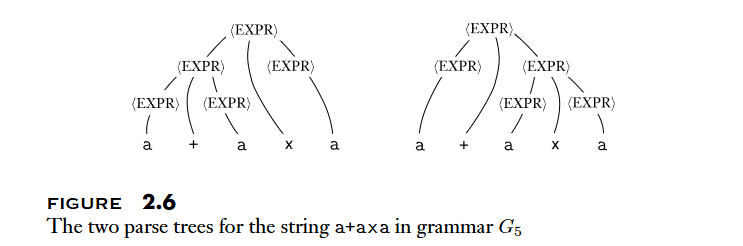
Inherently ambiguous: The context-free languages that can be generated only by ambiguous grammars. For example, $\{a^ib^jc^k~|~i = j~or~j = k\}$ .

Chomsky Normal Form

Definition

A context-free grammar is in Chomsky normal form if every rule is of the form $A → BC~or~A → a$ , where $a$ is any terminal and $A$ , $B$ , and $C$ are any variables except that $B$ and $C$ may not be the start variable. In addition we permit the rule $S → ε$ , where $S$ is the start variable.

如果原有的 grammar 包含 $S → ε$ ，則有兩種處理方式:

$L(G') = L(G) - \{ε\}$
允許 $S → ε$ rule

Theorem

Any context-free language is generated by a context-free grammar in Chomsky normal form.

證明: Convert any context-free grammar into Chomsky normal form:
1. Add a new start variable;
2. Eliminate all $ε$ rules ( $A → ε$ );
3. Handle all unit rules ( $A → B$ );
4. Convert all rules into the proper form.

Pushdown Automata

PDA: 下推自動機

Formal Definition of PDAs

Definition

A pushdown automaton is a 6-tuple $(Q, Σ, Γ, δ, q_0, F )$ ,where $Q$ , $Σ$ , $Γ$ , and $F$ are all finite sets, and

$Q$ is the set of states;
$Σ$ is the input alphabet;
$Γ$ is the stack alphabet;
$δ$ : $Q × Σ_ε × Γ_ε → P(Q × Γ_ε)$ is the transition function;
$q0 ∈ Q$ is the start state;
$F ⊆ Q$ is the set of accept states.

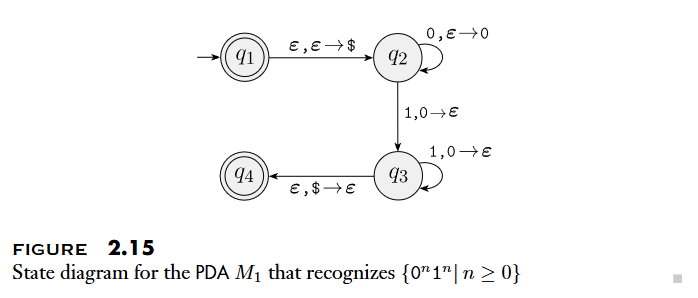
A pushdown automaton $M = (Q, Σ, Γ, δ, q_0, F )$ accepts input $w$ if $w$ can be written as $w = w_1w_2 ··· w_m$ , where $w_i ∈ Σ_ε$ and sequences of states $r_0, r_1, ··· , r_m ∈ Q$ and strings $s_0, s_1, ··· , s_m ∈ Γ^∗$ exist that satisfy the following three conditions. The stings $s_i$ represent the sequences of stack contents that $M$ has on the accepting branch of the computation.

$r_0 = q_0$ and $s_0 = ε$ ;
For $i = 0, ··· , m−1$ , we have $(r_{i+1}, b) ∈ δ(r_i, w_{i+1}, a)$ , where $s_i = at$ and $s_{i+1} = bt$ for some $a, b ∈ Γ_ε$ and $t ∈ Γ^∗$ ;
$r_m ∈ F$ .

Frequently used mechanisms:

Empty stack detection: $\$$ $$$ ;
- 使用一個不屬於 stack alphabet 的符號用來檢測 stack 是否為空，可以發現之前的範例，會在開始以及最後 push, pop 這個符號
Input end detection: Accept states.
- 為了與其他自動機統一格式而加上 Accept states 來判斷，實際上也是在檢測 stack 是否為空來判斷是否接受這個 string

Equivalence with CFGs

Theorem

A language is context free if and only if some pushdown automaton recognizes it.

Lemma

If a language is context free, then some pushdown automaton recognizes it.

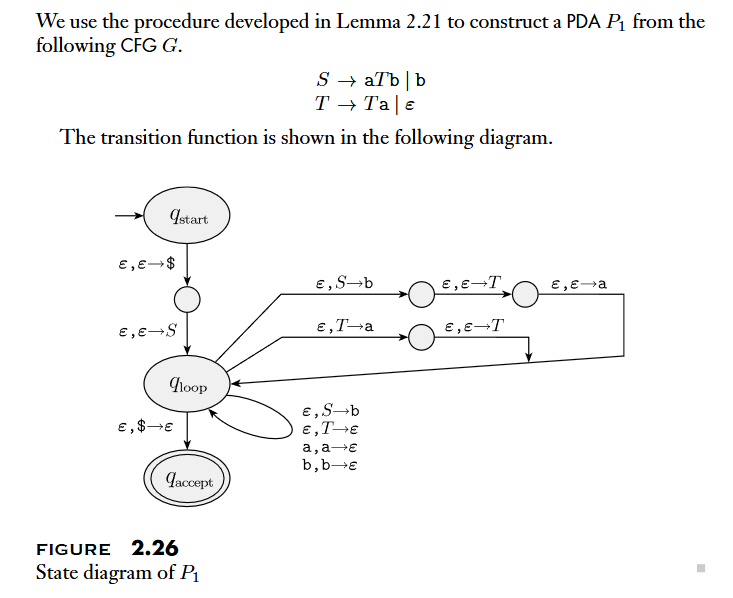
證明: Convert the given CFG into a PDA.
- 利用 PDA 的 nondeterminism 特性，用 leftmost derivation 產生所有可能的 substitution sequence，將 intermediate strings 儲存在 stack 中並且與 input string 進行對應，如果能到達 Accept states 代表能夠接受
- For the symbol on the stack top, two kinds of transitions:
  - For terminal $a$ , match the input: $a, a → ε$
  - For variable $A$ , apply the rule: $ε, A → w$

Lemma

If a pushdown automaton recognizes some language, then it is context free.

證明: Convert the given PDA into an equivalent CFG.
- 讓 PDA 的 each pair of states 產生一個 $A_{pq}$ 代表從 $p$ 到 $q$ 能夠產生的所有 strings
- Modify the PDA $P$ $P$ such that
  1. It has a single accept state, $q_{accept}$ $q_{a c c e p t}$ .
    - 將原有的 accept states 指向新的 $q_{accept}$ ( $ε$ arrow)
  2. It empties its stack before accepting.
    - 使用 $\$$ 符號
  3. Each transition either pushes a symbol onto the stack
    (a push move) or pops one off the stack (a pop move),
    but it does not do both at the same time.
    - 將 $a → b$ 拆為 $a → ε, ε → b$
- For a PDA $P = (Q, Σ, Γ, δ, q_0, \{q_{accept}\})$ $P = (Q, Σ, Γ, δ, q_{0}, {q_{a c c e p t}})$ , we construct a CFG $G = (V, Σ, R, S)$ $G = (V, Σ, R, S)$ with the following steps:
  1. $V = \{A_{pq}~|~p, q ∈ Q\}$
  2. $S = A_{q_0,q_{accept}}$
  3. $R$ $R$ contains the following three sets of rules:
    - For each $p, q, r, s ∈ Q$ $p, q, r, s \in Q$ , $t ∈ Γ$ $t \in Γ$ , and $a, b ∈ Σ_ε$ $a, b \in Σ_{ε}$ , if $(r, t) ∈ δ(p, a, ε)$ $(r, t) \in δ (p, a, ε)$ and $(q, ε) ∈ δ(s, b, t)$ $(q, ε) \in δ (s, b, t)$ , the rule $A_{pq} → aA_{rs}b$ $A_{p q} \to a A_{r s} b$
      - $t$ 進入到 stack 中，之後又被排出的過程
    - For each $p, q, r ∈ Q$ , the rule $A_{pq} → A_{pr}A_{rq}$
    - For each $p ∈ Q$ , the rule $A_{pp} → ε$

Claim

If $A_{pq}$ generates $x$ , then $x$ can bring $P$ from $p$ with empty stack to $q$ with empty stack.

證明: Induction on the number of steps in the derivation. (數學歸納法，從 state 轉移的角度來看)

Claim

If $x$ can bring $P$ from $p$ with empty stack to $q$ with empty stack, $A_{pq}$ generates $x$ .

證明: Induction on the number of steps in the computation. (數學歸納法，從 stack 的情況來看)

Corollary

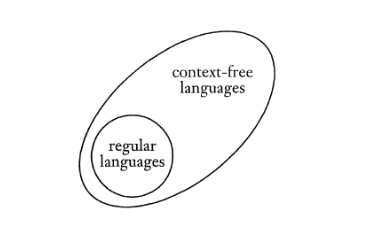
Every regular language is context free.
* NFA 可以視為 PDA 的特例

Non-Context-Free Languages

我們要如何去證明一個 Languages 是 Non-Context-Free Languages 呢?
ex: $B = \{ a^nb^nc^n~|~n ≥ 0 \}$ .

Pumping Lemma for CFLs

Theorem

If $A$ is a context-free language, then there is a number p (the pumping length) where, if $s$ is any string in $A$ of length at least $p$ , then $s$ may be divided into five pieces, $s = uvxyz$ satisfying the conditions:

for each $i ≥ 0$ , $uv^ixy^iz ∈ A$ ;
$|vy| > 0$ ; v, y 不同時為空字串
$|vxy| ≤ p$ .

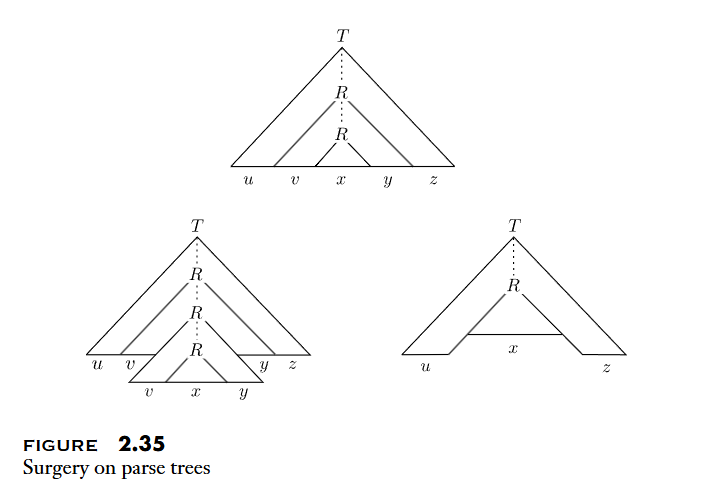
證明: 類似 Pumping Lemma for RL 的證明方式，透過鴿籠原理，當 parse tree 的樹高足夠時 (> variables 總數)，必定存在 variable R 在一條路徑中經過兩次以上，因此可以對其產生出的 string 進行 Pumping 而仍然屬於 CFL

注意:

context-free language 一定滿足 Pumping Lemma for CFLs
Pumping Lemma for CFLs 是 context-free language 的必要條件，不是充分條件
- 如果一個 language 滿足 Pumping Lemma for CFLs，其不一定為 context-free language

有了 Pumping Lemma for CFLs，我們可以利用反證法去證明一個 Languages 是 non-context-free languages:

Assume the language, say, $B$ , is context free in order to obtain a contradiction.
By the pumping lemma for CFLs, a pumping length p exists, and any string $w ∈ B$ can be pumped if $|w| ≥ p$ .
Find a string $s ∈ B$ , $|s| ≥ p$ , that $s$ cannot be pumped as described in the pumping lemma. 尋找反例
The contradiction is obtained, and therefore, $B$ is proved to be non-context-free.

Ogden’s Lemma for CFLs

Pumping Lemma for CFLs 的進階版

Theorem

If $A$ is a context-free language, then there is a number p where, if $s$ is any string in $A$ of length at least $p$ , in which we select any $p$ or more positions to be distinguished, then $s$ may be divided into five pieces, $s = uvxyz$ satisfying the conditions:

for each $i ≥ 0$ , $uv^ixy^iz ∈ A$ ;
$vy$ has at least one distinguished positions;
$vxy$ has at most $p$ distinguished positions.

如果挑選的 positions 是整個字串，就等價於 Pumping Lemma for CFLs

Example: $L = \{a^ib^jc^kd^l~|~i = 0~or~j = k = l \}$ .

使用 Pumping Lemma for CFLs 無法證明其為 non-context-free

Ogden’s Lemma for CFGs

Lemma

Let $G$ be a CFG. There exists a natural number p (depending on G) such that for all $s ∈ L(G)$ , if $s$ is marked so that it has $p$ or more distinguished positions, then there exists a variable $A$ and terminal strings $u, v, x, y, z$ satisfying the following conditions:

$s = uvxyz$ ;
either $v$ or $y$ has distinguished positions;
$vxy$ has no more than $p$ distinguished positions;
$S ⇒^* uAz$ ;
$A ⇒^* vAy$ ;
$A ⇒^* x$ ;
for each $i ≥ 0$ , $A ⇒^* v^ixy^i$ . 5 + 6

Inherently Ambiguous CFLs

證明 $L = \{a^ib^jc^k~|~i = j~or~j = k\}$ 是 Inherently Ambiguous，所有能夠產生它的 grammer 都是 Ambiguous 的

透過 Ogden’s Lemma for CFGs，可以證明不論用什麼 CFG 產生 $L$ ，其中的 $a^mb^mc^m$ 必定存在兩種不同的 parse trees，代表該 CFG 是 Ambiguous，故 $L$ 為 Inherently Ambiguous

Deterministic Context-Free Languages

[skip]

Properties of CFLs

Substitutions

is a generalization of the homomorphism we defined
in the study of regular languages

Homomorphism: $h : Σ → Π^∗$
Substitutions: $h : Σ → P(Π^∗)$ $h : Σ \to P (Π^{*})$
- 一個 symbol 可以對應到多個 string
can be extended in for strings and languages:
- $s: Σ^* → P(Π^∗)$ $s : Σ^{*} \to P (Π^{*})$
  - $s(ε) = ε$
  - $s(xa) = s(x)s(a)$
- $s: P(Σ^*) → P(Π^∗)$ $s : P (Σ^{*}) \to P (Π^{*})$
  - $s(L) = \{s(w)~|~w ∈ L\}$

Theorem

If $L$ is a CFL over $Σ$ , $s$ is a substitution on $Σ$ such that $s(a)$ is a CFL for each $a ∈ Σ$ , then $s(L)$ is also a CFL.

證明:
- Let $G = (V, Σ, R, S)$ $G = (V, Σ, R, S)$ be the CFG for $L$ $L$ and $G_a = (V_a, Σ_a, R_a, S_a)$ $G_{a} = (V_{a}, Σ_{a}, R_{a}, S_{a})$ be the CFG for $s(a)$ $s (a)$ , for each symbol $a ∈ Σ$ $a \in Σ$ . Construct a new grammar $G' = (V', Σ', R', S')$ $G^{'} = (V^{'}, Σ^{'}, R^{'}, S^{'})$ for $s(L)$ $s (L)$ :
  - $V'$ is the union of $V$ and all the $V_a$ ’s for $a ∈ Σ$ .
  - $Σ'$ is the union of all the $Σ_a$ ’s for $a ∈ Σ$ .
  - $R'$ $R^{'}$ consists of
    1. All rules in each $R_a$ ;
    2. The rule in $R$ but with each terminal a in their
      bodies replaced by $S_a$ everywhere a occurs.
- 將原有的 parse trees 後面接上 $s(a)$ 的 parse trees

Closure Properties

Let $A$ and $B$ be context-free languages. Let $R$ be a regular language. The results of the following operations are all context-free languages:

Substition: $s(A)$ ;
Union: $A ∪ B$ $A \cup B$ ;
- 證明: 加上 $S → S_A~|~S_B$
Concatenation: $AB$ $A B$ ;
- 證明: 加上 $S → S_AS_B$
Star: $A^∗$ $A^{*}$ ;
- 證明: 加上 $S_A → ε~|~S_AS_A$
Reversal: $A^R$ $A^{R}$ ;
- 證明: 將所有 rules 的 body 部分顛倒
Homomorphism: $h(A)$ $h (A)$ ;
- 證明: Substition 的特例
Inverse homomorphism: $h^{−1}(A)$ ;
† Intersection: $A ∩ R$ $A \cap R$ ;
- $A ∩ B$ 不一定是 context-free languages
- 證明: 類似合併兩 DFA 的方式，將 $A$ 的 PDA 和 $B$ 的 DFA 合併
† Difference: $A − R$ ( $A − R = A ∩ \overline R$ ).

$\overline A$ 不一定是 context-free languages

因為 $A ∪ B$ 為 context-free languages，但 $A ∩ B$ 不一定是 context-free languages，根據笛摩根定律，如果 $\overline A$ 是 context-free languages 會產生矛盾

Membership Test: CYK Algorithm

檢測 $w ∈ L?$

Let $G = (V, Σ, R, S)$ is the context-free grammar for $L$ in Chomsky normal form.
The input string $w = a_1a_2 ··· a_n$ is of length $n$ .
Construct the table with horizontal axis ( $i$ ) being the positions of the symbols in $w$ , $X_{ij}$ is the set of variables $A$ such that $A ⇒^* a_ia_{i+1} ··· a_j$ . We ask whether $S ∈ X_{1n}$ (i.e., $S ⇒^* a_1a_2 ··· a_n$ .)

Basis: $X_{ii}$ is the set of variables $A$ such that $A → a_i$ can be found in the rule.
Induction step: $X_{ij}$ $X_{i j}$ contains $A$ $A$ if we can find variables $B$ $B$ and $C$ $C$ , and integer $k$ $k$ such that
1. $i ≤ k < j$ ;
2. $B$ is in $X_{ik}$ ;
3. $C$ is in $X_{k+1,j}$ ;
4. $A → BC$ is a rule.
由下往上填滿，最後檢查 $S$ 有沒有在最上面的格子中
也能夠檢查 $w$ 的子串列是否也屬於 $L$ (對應的格子中是否有 $S$ )