正規語言-L2

正規語言相關文章參考資料為陳穎平教授上課講義

L2 Context-Free Languages

Context-Free Grammars

CFGs: 上下文無關文法，指的是字元在進行替換時不需要考慮上下文，其擁有足夠的表現力來表示大多數程式設計語言的語法

Formal Definition of CFGs

Definition

A context-free grammar is a 4-tuple $(V, \Sigma, R, S)$, where

1. $V$ is a finite set called the variables;
2. $\Sigma$ is a finite set, disjoint from $V$ ,called the terminals;
3. $R$ is a finite set of rules (or productions), with each rule being a variable and a string of variables and terminals;
4. $S \in V$ is the start variable.

Each rule consists of

• head: variable in $V$
• symbol →
• body: a string in $(V \cup \Sigma)^*$

• If $u, v, w \in (V \cup \Sigma)^*$, and $A \to w$ is a rule of the grammar, we say that $uAv$ yields $uwv$, written $uAv \Rightarrow uwv$.
• Say that $u$ derives $v$, written $u \Rightarrow^* v$, if $u = v$ or if a sequence $u_1, u_2, \cdots , u_k$ exists for $k \ge 0$ and $u \Rightarrow u_1 \Rightarrow u_2 \Rightarrow \cdots \Rightarrow v$ .
• The language of the grammar is $\{w \in \Sigma^*~|~S \Rightarrow^* w\}$.

Ambiguity

Leftmost derivation: A derivation of a string w in a grammar G is a leftmost derivation if at every step the leftmost remaining variable is the one replaced.

Definition

A string $w$ is derived ambiguously in context-free grammar $G$ if it has two or more different leftmost derivations. Grammar $G$ is ambiguous if it generates some string ambiguously.

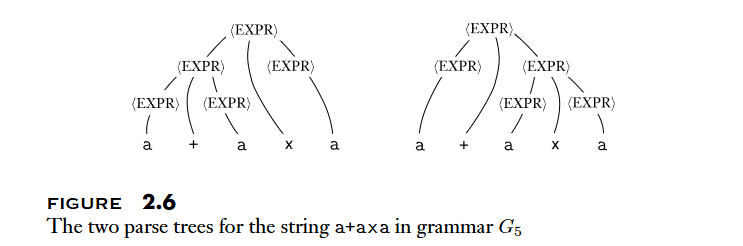
Inherently ambiguous: The context-free languages that can be generated only by ambiguous grammars. For example, $\{a^ib^jc^k~|~i = j~\text{or}~j = k\}$.

Chomsky Normal Form

Definition

A context-free grammar is in Chomsky normal form if every rule is of the form $A \to BC~\text{or}~A \to a$, where $a$ is any terminal and $A$, $B$, and $C$ are any variables except that $B$ and $C$ may not be the start variable. In addition we permit the rule $S \to \varepsilon$, where $S$ is the start variable.

如果原有的 grammar 包含 $S \to \varepsilon$，則有兩種處理方式:

1. $L(G') = L(G) - \{\varepsilon\}$
2. 允許 $S \to \varepsilon$ rule

Theorem

Any context-free language is generated by a context-free grammar in Chomsky normal form.

• 證明: Convert any context-free grammar into Chomsky normal form:
  1. Add a new start variable;
  2. Eliminate all $\varepsilon$ rules ($A \to \varepsilon$);
  3. Handle all unit rules ($A \to B$);
  4. Convert all rules into the proper form.

Pushdown Automata

PDA: 下推自動機

Formal Definition of PDAs

Definition

A pushdown automaton is a 6-tuple $(Q, \Sigma, \Gamma, \delta, q_0, F )$,where $Q$, $\Sigma$, $\Gamma$, and $F$ are all finite sets, and

1. $Q$ is the set of states;
2. $\Sigma$ is the input alphabet;
3. $\Gamma$ is the stack alphabet;
4. $\delta$ : $Q \times \Sigma_\varepsilon \times \Gamma_\varepsilon \to P(Q \times \Gamma_\varepsilon)$ is the transition function;
5. $q0 \in Q$ is the start state;
6. $F \subseteq Q$ is the set of accept states.

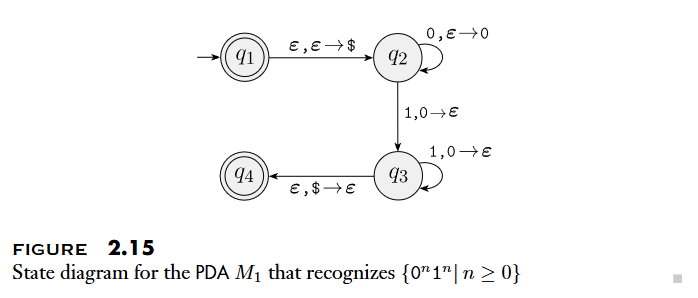
A pushdown automaton $M = (Q, \Sigma, \Gamma, \delta, q_0, F )$ accepts input $w$ if $w$ can be written as $w = w_1w_2 \cdots w_m$, where $w_i \in \Sigma_\varepsilon$ and sequences of states $r_0, r_1, \cdots , r_m \in Q$ and strings $s_0, s_1, \cdots , s_m \in \Gamma^*$ exist that satisfy the following three conditions. The stings $s_i$ represent the sequences of stack contents that $M$ has on the accepting branch of the computation.

1. $r_0 = q_0$ and $s_0 = \varepsilon$;
2. For $i = 0, \cdots , m-1$, we have $(r_{i+1}, b) \in \delta(r_i, w_{i+1}, a)$, where $s_i = at$ and $s_{i+1} = bt$ for some $a, b \in \Gamma_\varepsilon$ and $t \in \Gamma^*$;
3. $r_m \in F$ .

Frequently used mechanisms:

• Empty stack detection: $\$$;
  • 使用一個不屬於 stack alphabet 的符號用來檢測 stack 是否為空，可以發現之前的範例，會在開始以及最後 push, pop 這個符號
• Input end detection: Accept states.
  • 為了與其他自動機統一格式而加上 Accept states 來判斷，實際上也是在檢測 stack 是否為空來判斷是否接受這個 string

Equivalence with CFGs

Theorem

A language is context free if and only if some pushdown automaton recognizes it.

Lemma

If a language is context free, then some pushdown automaton recognizes it.

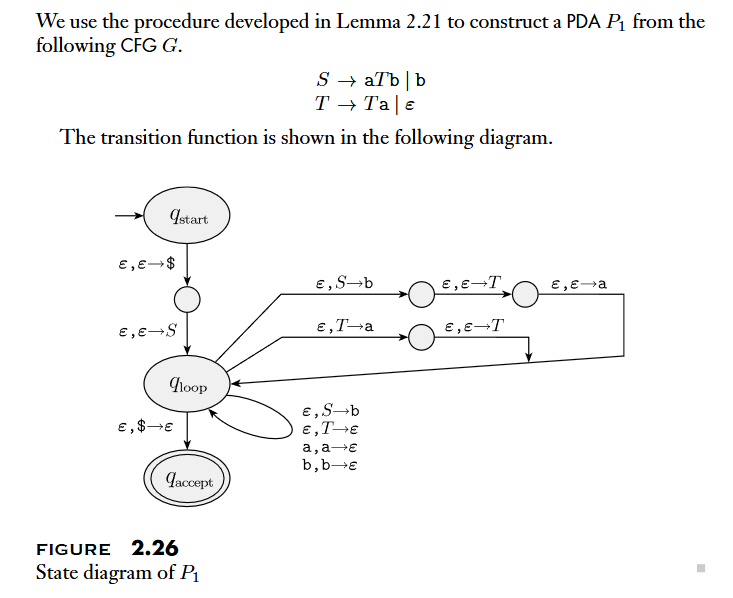
• 證明: Convert the given CFG into a PDA.
  • 利用 PDA 的 nondeterminism 特性，用 leftmost derivation 產生所有可能的 substitution sequence， 將 intermediate strings 儲存在 stack 中並且與 input string 進行對應，如果能到達 Accept states 代表能夠接受
  • For the symbol on the stack top, two kinds of transitions:
    • For terminal $a$, match the input: $a, ext{a} \to \varepsilon$
    • For variable $A$, apply the rule: $\varepsilon, ext{a} \to w$

Lemma

If a pushdown automaton recognizes some language, then it is context free.

• 證明: Convert the given PDA into an equivalent CFG.
  • 讓 PDA 的 each pair of states 產生一個 $A_{pq}$ 代表從 $p$ 到 $q$ 能夠產生的所有 strings
  • Modify the PDA $P$ such that
    1. It has a single accept state, $q_{accept}$.
       • 將原有的 accept states 指向新的 $q_{accept}$ ($\varepsilon$ arrow)
    2. It empties its stack before accepting.
       • 使用 $\$$ 符號
    3. Each transition either pushes a symbol onto the stack
       (a push move) or pops one off the stack (a pop move),
       but it does not do both at the same time.
       • 將 $a \to b$ 拆為 $a \to \varepsilon, \varepsilon \to b$
  • For a PDA $P = (Q, \Sigma, \Gamma, \delta, q_0, \{q_{accept}\})$, we construct a CFG $G = (V, \Sigma, R, S)$ with the following steps:
    1. $V = \{A_{pq}~|~p, q \in Q\}$
    2. $S = A_{q_0,q_{accept}}$
    3. $R$ contains the following three sets of rules:
       • For each $p, q, r, s \in Q$, $t \in \Gamma$, and $a, b \in \Sigma_\varepsilon$, if $(r, t) \in \delta(p, a, \varepsilon)$ and $(q, \varepsilon) \in \delta(s, b, t)$, the rule $A_{pq} \to aA_{rs}b$
         • $t$ 進入到 stack 中，之後又被排出的過程
       • For each $p, q, r \in Q$, the rule $A_{pq} \to A_{pr}A_{rq}$
       • For each $p \in Q$, the rule $A_{pp} \to \varepsilon$

Claim

If $A_{pq}$ generates $x$, then $x$ can bring $P$ from $p$ with empty stack to $q$ with empty stack.

• 證明: Induction on the number of steps in the derivation. (數學歸納法，從 state 轉移的角度來看)

Claim

If $x$ can bring $P$ from $p$ with empty stack to $q$ with empty stack, $A_{pq}$ generates $x$.

• 證明: Induction on the number of steps in the computation. (數學歸納法，從 stack 的情況來看)

Corollary

Every regular language is context free.
* NFA 可以視為 PDA 的特例

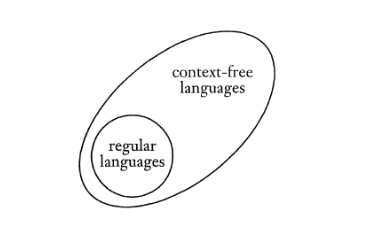
Non-Context-Free Languages

我們要如何去證明一個 Languages 是 Non-Context-Free Languages 呢?
ex: $B = \{ a^nb^nc^n~|~n \ge 0 \}$ .

Pumping Lemma for CFLs

Theorem

If $A$ is a context-free language, then there is a number p (the pumping length) where, if $s$ is any string in $A$ of length at least $p$, then $s$ may be divided into five pieces, $s = uvxyz$ satisfying the conditions:

1. for each $i \ge 0$, $uv^ixy^iz \in A$;
2. $|vy| > 0$; v, y 不同時為空字串
3. $|vxy| \le p$.

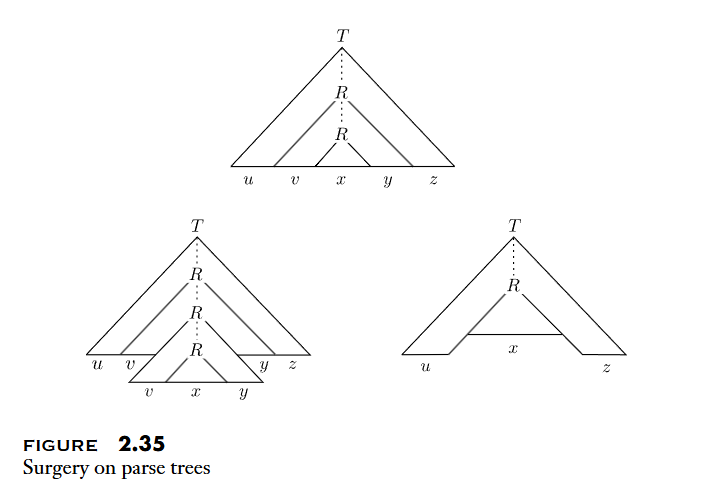
• 證明: 類似 Pumping Lemma for RL 的證明方式，透過鴿籠原理，當 parse tree 的樹高足夠時 (> variables 總數)，必定存在 variable R 在一條路徑中經過兩次以上，因此可以對其產生出的 string 進行 Pumping 而仍然屬於 CFL

注意:

• context-free language 一定滿足 Pumping Lemma for CFLs
• Pumping Lemma for CFLs 是 context-free language 的必要條件，不是充分條件
  • 如果一個 language 滿足 Pumping Lemma for CFLs，其不一定為 context-free language

有了 Pumping Lemma for CFLs，我們可以利用反證法去證明一個 Languages 是 non-context-free languages:

1. Assume the language, say, $B$, is context free in order to obtain a contradiction.
2. By the pumping lemma for CFLs, a pumping length p exists, and any string $w \in B$ can be pumped if $|w| \ge p$.
3. Find a string $s \in B$, $|s| \ge p$, that $s$ cannot be pumped as described in the pumping lemma. 尋找反例
4. The contradiction is obtained, and therefore, $B$ is proved to be non-context-free.

Ogden’s Lemma for CFLs

Pumping Lemma for CFLs 的進階版

Theorem

If $A$ is a context-free language, then there is a number p where, if $s$ is any string in $A$ of length at least $p$, in which we select any $p$ or more positions to be distinguished, then $s$ may be divided into five pieces, $s = uvxyz$ satisfying the conditions:

1. for each $i \ge 0$, $uv^ixy^iz \in A$;
2. $vy$ has at least one distinguished positions;
3. $vxy$ has at most $p$ distinguished positions.

• 如果挑選的 positions 是整個字串，就等價於 Pumping Lemma for CFLs

Example: $L = \{a^ib^jc^kd^l~|~i = 0~\text{or}~j = k = l \}$ .

• 使用 Pumping Lemma for CFLs 無法證明其為 non-context-free

Ogden’s Lemma for CFGs

Lemma

Let $G$ be a CFG. There exists a natural number p (depending on G) such that for all $s \in L(G)$, if $s$ is marked so that it has $p$ or more distinguished positions, then there exists a variable $A$ and terminal strings $u, v, x, y, z$ satisfying the following conditions:

1. $s = uvxyz$;
2. either $v$ or $y$ has distinguished positions;
3. $vxy$ has no more than $p$ distinguished positions;
4. $S \Rightarrow^* uAz$;
5. $A \Rightarrow^* vAy$;
6. $A \Rightarrow^* x$;
7. for each $i \ge 0$, $A \Rightarrow^* v^ixy^i$. 5 + 6

Inherently Ambiguous CFLs

證明 $L = \{a^ib^jc^k~|~i = j~\text{or}~j = k\}$ 是 Inherently Ambiguous，所有能夠產生它的 grammer 都是 Ambiguous 的

• 透過 Ogden’s Lemma for CFGs，可以證明不論用什麼 CFG 產生 $L$，其中的 $a^mb^mc^m$ 必定存在兩種不同的 parse trees，代表該 CFG 是 Ambiguous，故 $L$ 為 Inherently Ambiguous

Deterministic Context-Free Languages

[skip]

Properties of CFLs

Substitutions

is a generalization of the homomorphism we defined
in the study of regular languages

• Homomorphism: $h : \Sigma \to \Pi^*$
• Substitutions: $h : \Sigma \to P(\Pi^*)$
  • 一個 symbol 可以對應到多個 string
• can be extended in for strings and languages:
  • $s: \Sigma^* \to P(\Pi^*)$
    • $s(\varepsilon) = \varepsilon$
    • $s(xa) = s(x)s(a)$
  • $s: P(\Sigma^*) \to P(\Pi^*)$
    • $s(L) = \{s(w)~|~w \in L\}$

Theorem

If $L$ is a CFL over $\Sigma$, $s$ is a substitution on $\Sigma$ such that $s(a)$ is a CFL for each $a \in \Sigma$, then $s(L)$ is also a CFL.

• 證明:
  • Let $G = (V, \Sigma, R, S)$ be the CFG for $L$ and $G_a = (V_a, \Sigma_a, R_a, S_a)$ be the CFG for $s(a)$, for each symbol $a \in \Sigma$. Construct a new grammar $G' = (V', \Sigma', R', S')$ for $s(L)$:
    • $V'$ is the union of $V$ and all the $V_a$’s for $a \in \Sigma$.
    • $\Sigma'$ is the union of all the $\Sigma_a$’s for $a \in \Sigma$.
    • $R'$ consists of
      1. All rules in each $R_a$;
      2. The rule in $R$ but with each terminal a in their
         bodies replaced by $S_a$ everywhere a occurs.
  • 將原有的 parse trees 後面接上 $s(a)$ 的 parse trees

Closure Properties

Let $A$ and $B$ be context-free languages. Let $R$ be a regular language. The results of the following operations are all context-free languages:

• Substition: $s(A)$;
• Union: $A \cup B$;
  • 證明: 加上 $S \to S_A~|~S_B$
• Concatenation: $AB$;
  • 證明: 加上 $S \to S_AS_B$
• Star: $A^*$;
  • 證明: 加上 $S_A \to \varepsilon~|~S_AS_A$
• Reversal: $A^R$;
  • 證明: 將所有 rules 的 body 部分顛倒
• Homomorphism: $h(A)$;
  • 證明: Substition 的特例
• Inverse homomorphism: $h^{-1}(A)$;
• † Intersection: $A \cap R$;
  • $A \cap B$ 不一定是 context-free languages
  • 證明: 類似合併兩 DFA 的方式，將 $A$ 的 PDA 和 $B$ 的 DFA 合併
• † Difference: $A - R$ ($A - R = A \cap \overline R$).

$\overline A$ 不一定是 context-free languages

• 因為 $A \cup B$ 為 context-free languages，但 $A \cap B$ 不一定是 context-free languages，根據笛摩根定律，如果 $\overline A$ 是 context-free languages 會產生矛盾

Membership Test: CYK Algorithm

檢測 $w \in L?$

1. Let $G = (V, \Sigma, R, S)$ is the context-free grammar for $L$ in Chomsky normal form.
2. The input string $w = a_1a_2 \cdots a_n$ is of length $n$.
3. Construct the table with horizontal axis ($i$) being the positions of the symbols in $w$, $X_{ij}$ is the set of variables $A$ such that $A \Rightarrow^* a_ia_{i+1} \cdots a_j$. We ask whether $S \in X_{1n}$ (i.e., $S \Rightarrow^* a_1a_2 \cdots a_n$.)

• Basis: $X_{ii}$ is the set of variables $A$ such that $A \to a_i$ can be found in the rule.
• Induction step: $X_{ij}$ contains $A$ if we can find variables $B$ and $C$, and integer $k$ such that
  1. $i \le k < j$ ;
  2. $B$ is in $X_{ik}$ ;
  3. $C$ is in $X_{k+1,j}$ ;
  4. $A \to BC$ is a rule.
• 由下往上填滿，最後檢查 $S$ 有沒有在最上面的格子中
• 也能夠檢查 $w$ 的子串列是否也屬於 $L$ (對應的格子中是否有 $S$)