正規語言相關文章參考資料為陳穎平教授上課講義

L3 The Church-Turing Thesis

Turing Machines

圖靈機的想法: Finite control + unlimited and unrestricted memory.

在磁帶上面讀 & 寫
可以將讀取頭向左/右移動
磁帶是無限長的
可以立刻決定拒絕 (Reject) 或接受 (Accept)

Formal Definition of A Turing Machine

Definition

A Turing machine is a 7-tuple $(Q, Σ, Γ, δ, q_0, q_{accept}, q_{reject})$ , where $Q, Σ, Γ$ are all finite sets and

$Q$ is the set of states;
$Σ$ is the input alphabet not containing the blank symbol $⊔$ ;
$Γ$ $Γ$ is the tape alphabet, where $⊔ ∈ Γ$ $⊔ \in Γ$ and $Σ ⊆ Γ$ $Σ \subseteq Γ$ ;
- $Σ ⊆ Γ$ 是因為需要把 input string 放到磁帶上
- $⊔$ 代表空的位置
$δ$ $δ$ : $Q × Γ → Q × Γ × \{ L, R \}$ $Q \times Γ \to Q \times Γ \times {L, R}$ is the transition function;
- $\{ L, R \}$ 用於控制磁帶頭左/右移
$q_0 ∈ Q$ is the start state;
$q_{accept} ∈ Q$ is the accept state;
$q_{reject} ∈ Q$ is the reject state.

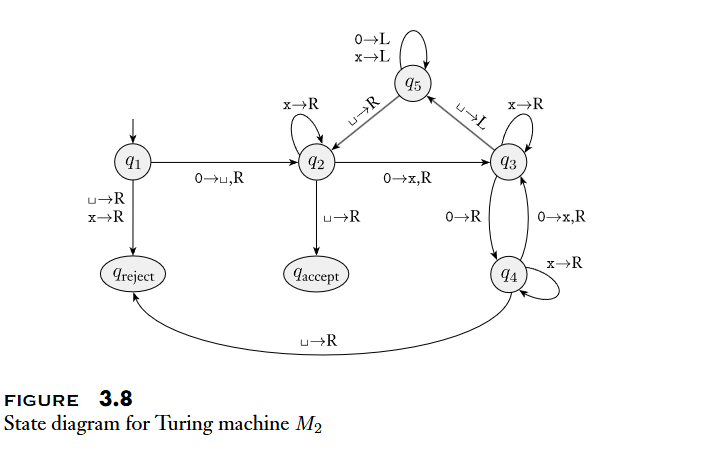
A configuration of the Turing machine consists of

the current state;
the current tape contents;
the current head location.

and is represented as $uqv$ for a state $q$ , two strings $u$ and $v$ over the tape alphabet $Γ$ , and the current head at the first symbol of $v$ .

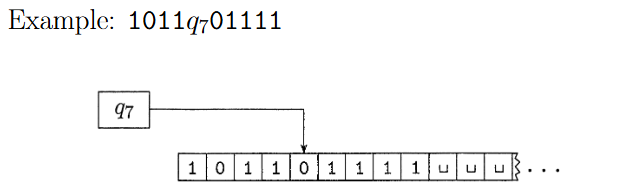
If the Turing machine can legally go from configuration $C_1$ to configuration $C_2$ , we say that $C_1$ yields $C_2$ .

Formally, if $a, b, c ∈ Γ$ , $u, v ∈ Γ^∗$ , and $q_i, q_j ∈ Q$ , $uaqibv$ and $uqjacv$ are two configurations.

$ua~q_i~bv$ yields $u~q_j~acv$ if $δ(q_i, b) = (q_j, c, L)$ .
$ua~q_i~bv$ yields $uac~q_j~v$ if $δ(q_i, b) = (q_j, c, R)$ .

A Turing machine $M$ accepts input $w$ if a sequence of configurations $C_1, C_2, ... , C_k$ exists, where

$C_1$ is the start configuration of $M$ on input $w$ ;
Each $C_i$ yields $C_{i+1}$ ;
$C_k$ is an accepting configuration.

The collection of strings that $M$ accepts is the language of $M$ , or the language recognized by $M$ , denoted $L(M)$ .

Definition

Call a language Turing-recognizable if some Turing machine recognizes it. (Also known as recursively enumerable language)

Definition

Call a language Turing-decidable or simply decidable if some Turing machine decides it. (Also known as recursive language)

recognizes: 可能會有字串不屬於 accept/reject，在圖靈機中不斷循環
decides: 字串一定屬於 accept/reject
因此 Turing-recognizable 的範圍比 Turing-decidable 大

Variants of Turing Machines

Multitape Turing Machines

k-tape Turing machine:

$δ$ : $Q × Γ^k → Q × Γ^k × \{ L, R, S \}^k$ .
有 k 個磁帶可以操作
每個磁帶頭可以選擇向左/右或是不動

Theorem

Every multitape Turing machine has an equivalent single-tape Turing machine.

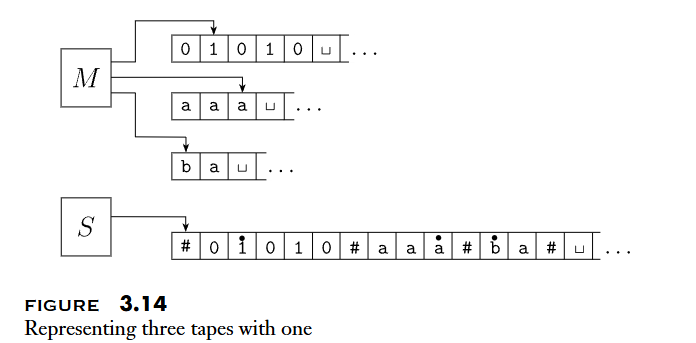
single-tape Turing machine 可以視為 multitape Turing machine 的特例: $k=1$
可以使用 single-tape Turing machine 來模擬 multitape Turing machine 的行為
- 用 $\#$ 符號分隔每個 tape 的資料
- 使用 dotted tape symbols 代表該磁帶的磁帶頭所在位置
- 每次掃過每個 tape 並記錄磁帶頭位置，透過 transition function 模擬行為，並對對應的 tape 進行操作

Corollary

A language is Turing-recognizable if and only if some multitape Turing machine recognizes it.

Nondeterministic Turing Machines

Nondeterministic - several choices at any point:

$δ$ $δ$ : $Q × Γ → P(Q × Γ × \{ L, R \})$ $Q \times Γ \to P (Q \times Γ \times {L, R})$ .
- transition function 改為 Power set

Theorem

Every nondeterministic Turing machine has an equivalent deterministic Turing machine.

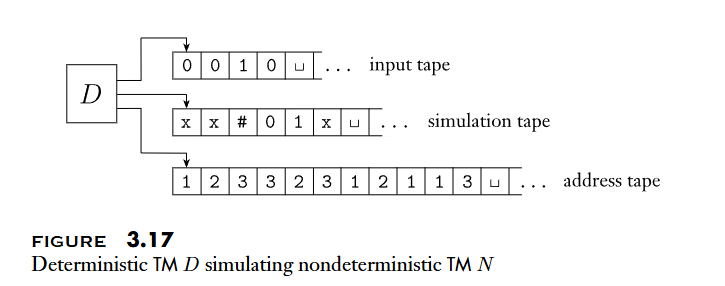
deterministic Turing machine 可以視為 nondeterministic Turing machine 的特例
把 deterministic Turing machine 當作一個 queue 使用，用來儲存 nondeterministic Turing machine 的狀態
- 用 $\#$ 符號分隔每個狀態
- 類似 BFS 遍歷 nondeterministic Turing machine 的所有可能

Corollary

A language is Turing-recognizable if and only if some nondeterministic Turing machine recognizes it.

Corollary

A language is decidable if and only if some nondeterministic Turing machine decides it.

Enumerators

枚舉器: 枚舉所有字串

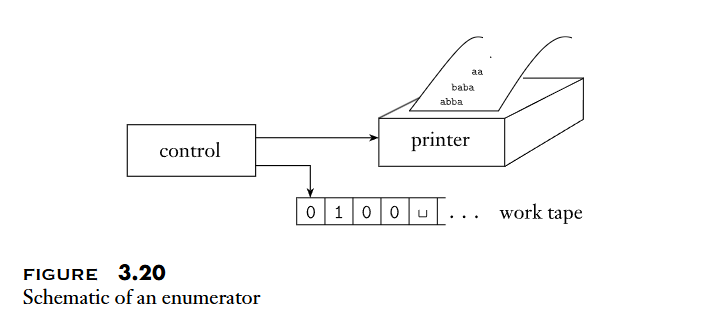Theorem

A language is Turing-recognizable if and only if some enumerator enumerates it.

The Definition of Algorithm

Hilbert’s Problems

Find an algorithm to determine whether a given polynomial Diophantine equation with integer coefficients has an integer solution.

如何定義 algorithm ?
- Church: λ-calculus;
- Turing: Turing machines.

Terminology for Describing Turing Machines

The different levels of detail:

formal description: Spells out in full the Turing machine’s states, transition function, and so on;
- 可以想像成 machine code/assembly code
implementation description: Describes the way that the Turing machine moves its head and the way that it stores data on its tape;
- 可以想像成 C/Java code
high-level description: Describes an algorithm.
- 可以想像成 pseudo code