正規語言相關文章參考資料為陳穎平教授上課講義

L4 Decidability

Decidable Languages

Decidable Problems Concerning Regular Languages

定義 $A_{DFA} = \{ ⟨B, w⟩~|~B~is~a~DFA~that~accepts~input~string~w \}$

Theorem

$A_{DFA}$ is a decidable language.

證明: 建立一個 TM $M$ 模擬 $w$ 在 $B$ 上的行為，如果停在 accept states 則 $A_{DFA}$ appect，否則會 reject，只有這兩種可能，因此是 Decidable 的

定義 $A_{NFA} = \{ ⟨B, w⟩~|~B~is~a~NFA~that~accepts~input~string~w \}$

Theorem

$A_{NFA}$ is a decidable language.

證明: 建立一個 TM $N$ ，並建立與 $B$ 等價的 DFA $C$ ，可以將 $⟨C, w⟩$ 帶入 TM $M$ 去判斷是 accept or reject

定義 $A_{REX} = \{ ⟨R, w⟩~|~R~is~a~regular~expression~that~generates~string~w \}$

Theorem

$A_{REX}$ is a decidable language.

證明: 建立一個 TM $P$ ，並建立與 $R$ 等價的 NFA $A$ ，可以將 $⟨A, w⟩$ 帶入 TM $N$ 去判斷是 accept or reject

定義 $E_{DFA} = \{ ⟨A⟩~|~A~is~a~DFA~and~L(A) = ∅ \}$

Theorem

$E_{DFA}$ is a decidable language.

證明: 建立一個 TM $T$ ，從 start state 開始進行 BFS 並 mark 已經被經過的 states，如果有到達 accept states 則 reject，否則 accept (沒有 string 會被 $A$ accept)

定義 $EQ_{DFA} = \{ ⟨A, B⟩~|~A~and~B~are~DFAs~and~L(A) = L(B) \}$

Theorem

$EQ_{DFA}$ is a decidable language.

證明: 建立一個 TM $F$ ，根據某些操作在 DFA 上的封閉性，可以建立一個 DFA $C$ 使得 $L(C) = (L(A)∩\overline {L(B)})∪(\overline {L(A)}∩L(B))$ ，代表是兩個 language 的對稱差，可以將 $⟨C⟩$ 帶入 TM $T$ 去判斷其 language 是否為空，如果 TM $T$ 是 accept 則 accept，否則 reject (對稱差不為空)

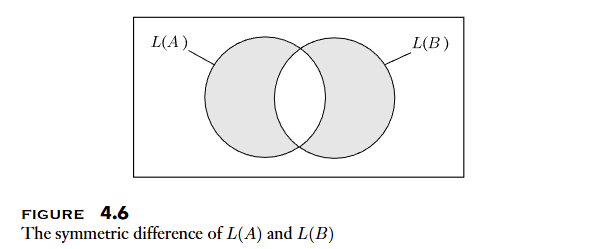
Decidable Problems Concerning Context-Free Languages

定義 $A_{CFG} = \{ ⟨G, w⟩~|~B~is~a~CFG~that~generates~string~w \}$

Theorem

$A_{CFG}$ is a decidable language.

證明: 建立一個 TM $S$ $S$ ，先將 $G$ $G$ 轉換為等價的 Chomsky normal form，如果 $w$ $w$ 的長度為 n (不為 0)，則在 2n - 1 步內一定可以判斷是否能產生 $w$ $w$ ，如果能產生則 accept，否則 reject
- 也能輕易地用 CYK Algorithm 來判斷

定義 $E_{CFG} = \{ ⟨G⟩~|~G~is~a~CFG~and~L(G) = ∅ \}$

Theorem

$E_{CFG}$ is a decidable language.

證明: 建立一個 TM $R$

定義 $EQ_{CFG} = \{ ⟨G, H⟩~|~G~and~H~are~CFGs~and~L(G) = L(H) \}$

$EQ_{CFG}$ is Undecidable (Chapter 5)

Theorem

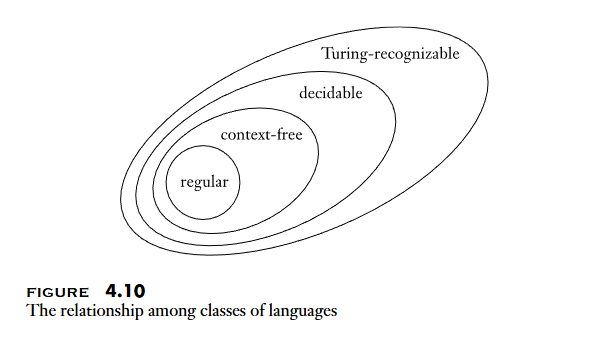
Every context-free language is decidable.

證明:

最後可以得到這樣的關係:

The Halting Problem

Is there any problem algorithmically unsolvable?

定義 $A_{TM} = \{ ⟨M, w⟩~|~M~is~a~TM~that~accepts~w \}$

Theorem

$A_{TM}$ is undecidable.

證明: 之後證明

$A_{TM}$ is Turing-recognizable.

證明: 建立一個 TM $U$ 模擬 $w$ 在 $M$ 上的行為，如果能到達 accept state 則 accept，如果到達 reject state 則 reject (有可能卡在 loop)

The Diagonalization Method

Measuring the sizes of infinite sets.

假設有兩個 set $A, B$ ，如果能找到一個函數 $f$ from $A$ to $B$ ，並滿足:

one-to-one: $ x ≠ y ⇒ f (x) ≠ f (y)$
onto: $ ∀b ∈ B, ∃a ∈ A, f (a) = b$

則 $A, B$ 為 same size，並且 $f$ 稱為 correspondence

Definition

A set $A$ is countable if either it is finite or it has the same size as $N$ .

Theorem

$R$ is uncountable.

證明: 先假設實數集合 $R$ $R$ 是 countable 的，則存在函數 $f$ $f$ 使得 $N$ $N$ 與其內元素一一對應，我們可以找到一個實數 $x$ $x$ 是沒有被對應的的，產生矛盾
- $x$ 的產生方式: 取 i 對應元素的小數點後第 i 位，並改變其數值

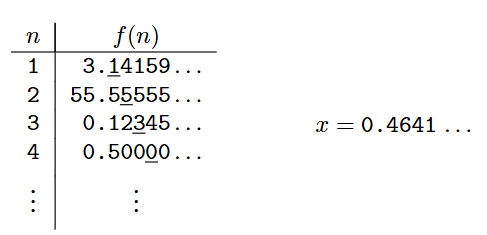Corollary

Some languages are not Turing-recognizable.

證明: 利用 Diagonalization Method

The Halting Problem Is Undecidable

證明 $A_{TM}$ is undecidable.

A Turing-Unrecognizable Language

A language is co-Turing-recognizable if it is the complement of a Turing-recognizable language.

Theorem

A language is decidable iff it is Turing recognizable and co-Turing-recognizable.

證明: 建立一個 TM $M$ $M$ ，當接收 string $w$ $w$ 後，同時模擬 $M_1, M_2$ $M_{1}, M_{2}$ 的行為，如果 $M_1$ $M_{1}$ accept 則 accept，如果 $M_2$ $M_{2}$ accept 則 reject (可以避免卡在 loop)
- $M_1$ 是 Turing recognizable 所對應的 TM
- $M_2$ 是 co-Turing-recognizable 所對應的 TM
- 不可能兩者同時卡在 loop