正規語言-L5

正規語言相關文章參考資料為陳穎平教授上課講義

L5 Reducibility

If problem A reduces to problem B, we can use a solution to B to solve A.

When A is reducible to B, solving A cannot be harder than solving B because a solution to B gives a solution to A. Therefore, if A is reducible to B,

• B is decidable ⇒ A is decidable;
• A is undecidable ⇒ B is undecidable.

Undecidable Problems from Language Theory

定義 $HALT_{TM} = \{ ⟨M, w⟩~|~M~is~a~TM~and~M~halts~on~input~w \}$

Theorem

$HALT_{TM}$ is undecidable.

• 證明: 假設 $HALT_{TM}$ 的 decider $R$ 存在，則可以利用 $R$ 建立 $A_{TM}$ 的 decider $S$，產生矛盾

---

定義 $E_{TM} = \{ ⟨M⟩~|~M~is~a~TM~and~L(M) = ∅ \}$

Theorem

$E_{TM}$ is undecidable.

• 證明: 假設 $E_{TM}$ 的 decider $R$ 存在，則可以利用 $R$ 建立 $A_{TM}$ 的 decider $S$，產生矛盾

---

定義 $REGULAR_{TM} = \{ ⟨M⟩~|~M~is~a~TM~and~L(M)~is~a~regular~language \}$

Theorem

$REGULAR_{TM}$ is undecidable.

• 證明: 假設 $REGULAR_{TM}$ 的 decider $R$ 存在，則可以利用 $R$ 建立 $A_{TM}$ 的 decider $S$，產生矛盾

---

Theorem

Rice’s theorem: Let $P$ be a language consisting of Turing machine descriptions where $P$ fulfills two conditions.
First, $P$ is nontrivial: it contains some, but not all, TM descriptions.
Second, $P$ is a property of the TM’s language: whenever $L(M_1) = L(M_2)$, we have $⟨M_1⟩ ∈ P~iff~⟨M_2⟩ ∈ P$ . Here $M_1$ and $M_2$ are any TMs.
Prove that $P$ is an undecidable language.

---

定義 $EQ{TM} = \{ ⟨M_1, M_2⟩~|~M_1~and~M_2~are~TMs~and~L(M_1) = L(M_2) \}$

Theorem

$EQ_{TM}$ is undecidable.

• 證明: 假設 $EQ_{TM}$ 的 decider $R$ 存在，則可以利用 $R$ 建立 $E_{TM}$ 的 decider $S$，產生矛盾

Reductions via Computation Histories

The computation history for a Turing machine on an input is simply the sequence of configurations that the machine goes through as it processes the input.

Definition

An accepting computation history for $M$ on $w$ is a sequence of configurations, $C_1, C_2, ... , C_l$, where $C_1$ is the start configuration of $M$ on $w$, $C_l$ is an accepting configuration of $M$ , and each $C_i$ legally follows from $C_{i−1}$ according to the rules of $M$ .

A rejecting computation history for $M$ on $w$ is defined similarly, except that $C_l$ is a rejecting configuration.

Definition

A linear bounded automaton is a restricted type of Turing machine wherein the tape head isn’t permitted to move off the portion of the tape containing the input. (除了 input 之外不需要額外空間)

---

Lemma

Let $M$ be an LBA with $q$ states and $g$ symbols in the tape alphabet. There are exactly $qng^n$ distinct configurations of $M$ for a tape of length $n$.

定義 $A_{LBA} = \{ ⟨M, w⟩~|~M~is~a~LBA~that~accepts~input~string~w \}$

Theorem

$A_{LBA}$ is decidable.

• 證明: 因為 LBA 的 configurations 是有限的，因此我們可以判斷它是否進入循環

---

定義 $E_{LBA} = \{ ⟨M⟩~|~M~is~an~LBA~and~L(M) = ∅ \}$

Theorem

$E_{LBA}$ is undecidable.

• 證明: 可以建立一個 LBA $B$，輸入 TM 的 computation history 並檢驗，如果是 accepting computation history 的話則 accept，否則 reject

---

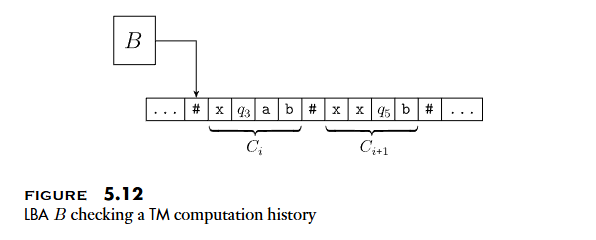
定義 $ALL_{CFG} = \{ ⟨G⟩~|~G~is~a~CFG~and~L(G) = Σ^∗ \}$

Theorem

$ALL_{CFG}$ is undecidable.

• 證明:
  • 給定 TM $M$ 以及 input $w$，可以建立一個 PDA $D$，$D$ 會 accept 除了 $w$ 在 $M$ 的 accepting computation histories 之外的所有 strings
  • 則 PDA $D$ 對應的 CFG $G$ 會產生 $Σ^∗$ iff $M$ not accept $w$
  • 可以利用 $ALL_{CFG}$ 去判斷 $L(G)$ 是否為 $Σ^∗$ 去得出 $M$ 是否 accept $w$

$G$ generates all strings

A Simple Undecidable Problem

Post correspondence problem (PCP)
To determine whether a collection of dominos has a match.

A collection of dominos:
$\{[\frac{b}{ca}],[\frac{a}{ab}],[\frac{ca}{a}],[\frac{abc}{c}]\}$

A match (abcaaabc):
$[\frac{a}{ab}],[\frac{b}{ca}],[\frac{ca}{a}],[\frac{a}{ab}],[\frac{abc}{c}]$

Formally, an instance of PCP is a collection $P$ of dominos:
$\{[\frac{t_1}{b_1}],[\frac{t_2}{b_2}],...,[\frac{t_k}{b_k}]\}$
and a match is a sequence $i_1, i_2, ... , i_l$, where $t_{i_1}t_{i_2} ··· t_{i_l} = b_{i_1}b_{i_2} ··· b_{i_l}$. The problem is to determine whether $P$ has a match.

定義 $PCP = \{ ⟨P⟩~|~P~is~an~instance~of~PCP~with~a~match \}$

Theorem

$PCP$ is undecidable.

• 證明: 略

Mapping Reducibility

Being able to reduce problem $A$ to problem $B$ by using a mapping reducibility means that a computable function, called a reduction, exists that converts instances of problem $A$ to instances of problem $B$.

Computable Functions

A Turing machine computes a function by starting with the input to the function to the tape and halting with the output of the function on the tape.

Definition

A function $f: Σ^∗ → Σ^∗$ is a computable function if some Turing machine $M$, on every input $w$, halts with just $f(w)$ on its tape.

Formal Definition of Mapping Reducibility

Definition

Language $A$ is mapping reducible to language $B$, written $A ≤_m B$, if there is a computable function $f: Σ^∗ → Σ^∗$, where for every $w$, $w ∈ A ⇔ f(w) ∈ B$ .
The function $f$ is called the reduction of $A$ to $B$.

Theorem

If $A ≤_m B$ and $B$ is decidable, then $A$ is decidable.

• 證明: 假設 $B$ 的 decider $M$ 存在，則可以利用 $M$ 以及 computable function $f$ 建立 $A$ 的 decider $N$

Corollary

If $A ≤_m B$ and $A$ is undecidable, then $B$ is undecidable.

ex:

---

Theorem

If $A ≤_m B$ and $B$ is Turing-recognizable, then $A$ is Turing-recognizable.

• 證明: 類似 decidable 的證明

Corollary

If $A ≤_m B$ and $A$ is not Turing-recognizable, then $B$ is not Turing-recognizable.

Theorem

$EQ_{TM}$ is neither Turing-recognizable nor co-Turing-recognizable.

---

There are only the following situations are possible for a language $A$ and its complement $\overline A$

• $A$ and $\overline A$ are both decidable.
• Neither $A$ nor $\overline A$ is Turing-recognizable.
• $A$ is Turing-recognizable but undecidable, and $\overline A$ is not Turing-recognizable.

統整

• decidable or not:

  	DFA	CFG	LBA	TM
  A	O	O	O	X
  E	O	O	X	X
  EQ	O	X	X	X

• $HALT_{TM}, REGULAR_{TM}, ALL_{CFG}, MPCP, PCP$ is undecidable.

• $\overline {A_{TM}}, L_d$ is not Turing-recognizable.