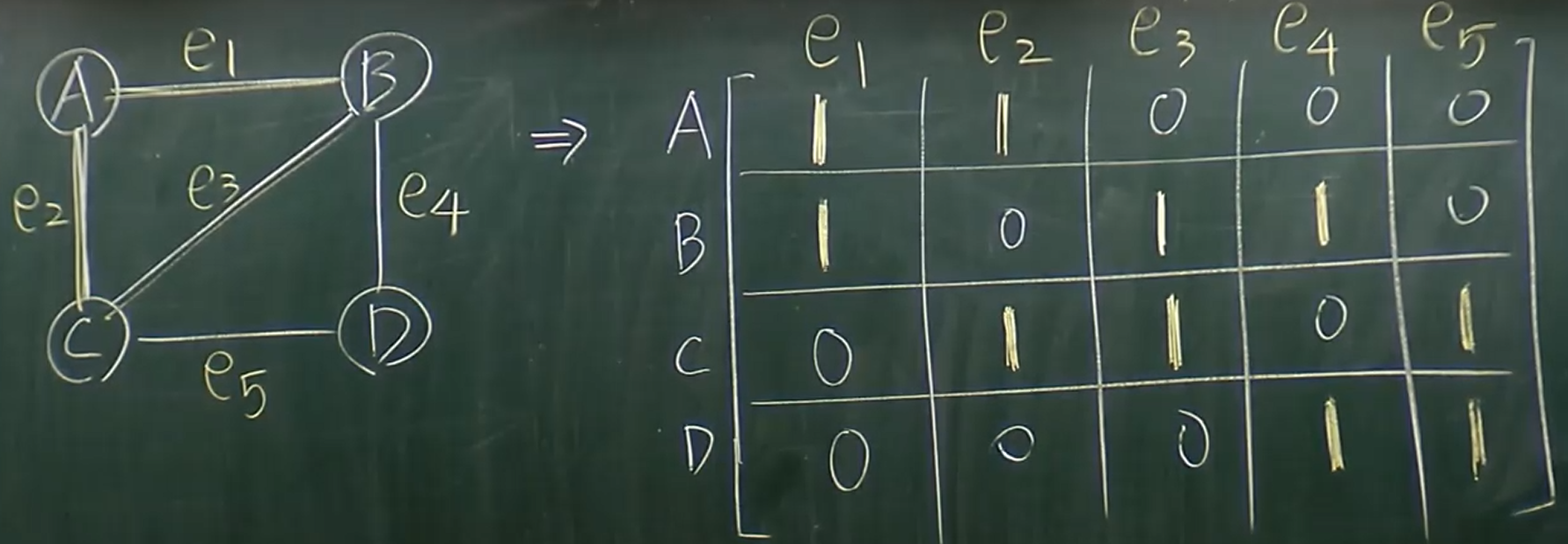資料結構-圖

考研相關文章參考資料為 wjungle 大神提供的筆記

Graph

• 令 $G = <V, E>$ 代表圖形是由兩個非空集合組成:
  • $V$: 代表頂點 (Vertex)
  • $E$: 代表邊 (Edge)
• 根據邊的類型，可分為兩類:
  • Undirected Graph (無向圖)
    • 邊不具有方向性
    • $(i,j) = (j,i)$ 代表同一邊
  • Directed Graph (有向圖)
    • 邊具有方向性
    • $(i,j) \neq (j,i)$

相關術語

• Eulerian cycle (尤拉 cycle)
  • 從某點出發，經過每個邊各一次，又回到原點
  • 充分必要條件: 每個頂點之 degree 為偶數
• Eulerian chain
  • 從某點出發，經過每個邊各一次，不一定要回到原點
  • 充分必要條件: 有兩個頂點之 degree 為奇數，剩餘頂點之 degree 為偶數
• Hamiltonian Path (漢米爾頓路徑)
  • 從某點出發，經過每個頂點各一次，不一定要回到原點
  • Hamiltonian cycle: 要回到原點

---

• Complete Graph (完全圖)
  • 具有最多邊數的圖
  • $n$ 個頂點的無向圖: $\frac{n(n-1)}{2}$ 條邊
  • $n$ 個頂點的有向圖: $n(n-1)$ 條邊
• Subgraph & Component (子圖)
• Path
• Path length
  • 路徑上的邊數
• Single Path
  • 除了起點與終點可能相同之外，中間經過的頂點皆不相同
  • ex:
    • 1-2-3-4 (O)
    • 1-2-3-4-1 (O)
    • 1-2-3-2-4 (X)
• Cycle
  • 起點與終點相同的 Single Path
  • ex: 1-2-3-4-1
• Connected (連通)
  • 對無向圖而言，任意頂點對之間皆有 Path 存在
  • Tree 可視為一個 Connected 無向圖
    • Connected 無向圖不可視為一顆 Tree: 可能會有 cycle
    • 無 cycle 無向圖不可視為一顆 Tree: 可能不連通
• Connected Component (連通子圖)
• Strongly Connected (強連通)
  • 對無向圖而言，任意頂點對 $(i,j)$ 滿足:
    • $i$ 有 Path 可到達 $j$
    • $j$ 有 Path 可到達 $i$
• Strongly Connected Component (強連通子圖)
• Degree (分支度)
  • 無向圖: 該頂點連結的邊數
    • $|E| = \frac{1}{2}\sum{Degree}$
  • 有向圖分為:
    • Out-Degree (出支度): 頂點射出之邊數
    • In-Degree (入支度): 射入頂點之邊數
    • $|E| = \sum{OutDegree}= \sum{InDegree}$

Graph 的表示方法

Adjacency Matrix (相鄰矩陣)

• 令 $G = <V,E>,~|V| = n$，則準備一個 matrix $A:n * n$，其中 $A[i, j]=$
  • $1,~if$ 邊 $(i,j)$ 存在
  • $0,~if$ 不存在
• 無向圖
  • 相鄰矩陣必為對稱矩陣 (Symmetric)
    • $(i,j) = (j,i) \Rightarrow A[i,j] = A[j,i]$
  • 判斷邊是否存在: $O(1)$
    • 查 $A[i,j]$
  • 求頂點 $V_i$ 之 degree: $O(n)$
    • 查第 $i$ 行/列元素和
  • 求圖之邊數: $O(n^2)$
    • $\frac{1}{2}\sum{Degree} = \frac{1}{2}\sum{\sum{A[i,j]}}$
• 有向圖
  • 行為 In-Degree，列為 Out-Degree
  • 相鄰矩陣不一定為對稱矩陣 (Symmetric)
  • 判斷邊是否存在: $O(1)$
  • 求頂點 $V_i$ 之 In/Out-degree: $O(n)$
    • 查第 $i$ 行/列元素和
  • 求圖之邊數: $O(n^2)$
    • $\sum{InDegree} = \sum{OutDegree} = \sum{\sum{A[i,j]}}$

Adjacency Lists (相鄰串列)

• 令 $G = <V,E>,~|V| = n,~|E| = e$，則準備 $n$ 條相鄰串列，以 $Vertex[1...n]$ of pointer 表示，其中 $Vertex[i]$ 代表 $V_i$ 之相鄰串列，記錄所有與 $V_i$ 相鄰之頂點編號
  • Node: Vertex No. | Next (Link)
• 無向圖
  • 所有相鄰串列之 Node 總數 = $2|E|$
    • 一條邊會加入兩個相鄰串列的 Node
  • 判斷邊是否存在: $O(V_i~串列長度) \leq O(|E|)$
    • 檢查 $Vertex[i]$ 串列中是否存在 Node $V_j$
  • 求頂點 $V_i$ 之 degree: $O(V_i~串列長度) \leq O(|E|)$
    • 求 $Vertex[i]$ 串列長度
  • 求圖之邊數: $O(|V|+|E|)$
    • $\frac{1}{2}\sum{Degree} = \frac{1}{2}\sum{V_i~串列長度}$
• 有向圖
  • 所有相鄰串列之 Node 總數 = $|E|$
  • 判斷邊是否存在: $O(V_i~串列長度) \leq O(|E|)$
  • 求頂點 $V_i$ 之 degree:
    • Out-Degree: $O(V_i~串列長度) \leq O(|E|)$ 求 $Vertex[i]$ 串列長度
    • In-Degree: $O(|V|+|E|)$ 求所有串列中 Node $V_i$ 出現次數
  • 求圖之邊數: $O(|V|+|E|)$
    • $\sum{OutDegree} = \sum{V_i~串列長度}$

比較表

• 令 $G = <V,E>,~|V| = n,,~|E| = e$

	Adjacency Matrix	Adjacency Lists
空間需求	$O(n^2)$	$O(n+e)$
邊數少	不適合 (稀疏矩陣)	適合
邊數多	適合	不適合
判斷邊是否存在	適合 $O(1)$	不適合 $O(e)$
求邊數、連通與否…	不適合 $O(n^2)$	適合 $O(n+e)$

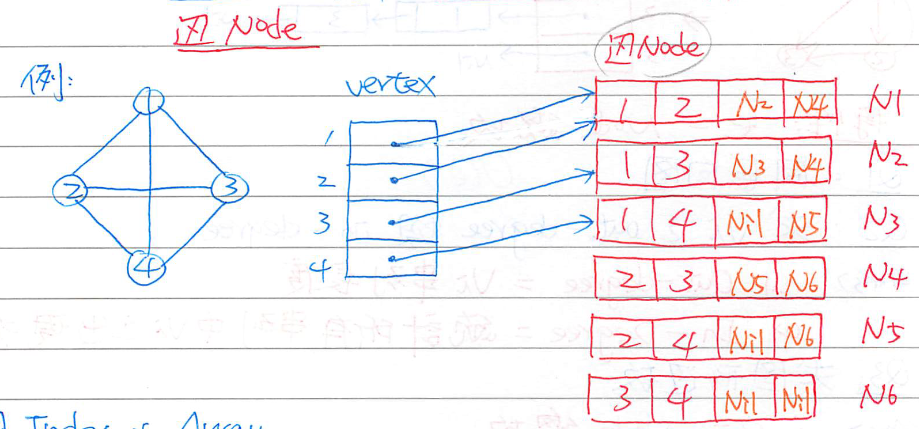
Adjacency Multilists (相鄰多元陣列)

• 令 $G = <V,E>,~|V| = n,,~|E| = e$，圖中的每條邊用一個 Node 來表示
  • Node: $V_i$ | $V_j$ | Link for $V_i$ | Link for $V_j$
    • Link for $V_i$: 指向下一個包含 $V_i$ 的 Node
    • Link for $V_j$: 指向下一個包含 $V_j$ 的 Node
  • 另準備一個 $Vertex[1...n]$ of pointer，其中 $Vertex[i]$ 指向第一個包含 $V_i$ 的 Node
• 空間需求: $O(|V|+|E|)$

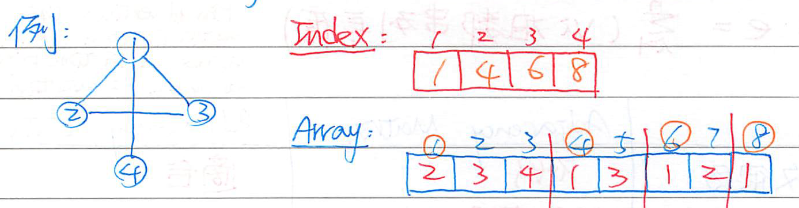
Index Array

• 用一個 Array 紀錄所有點之相鄰節點編號，且用一個 Index 告知其起始位置
• 空間需求: $O(|V|+|E|)$

Incident Matrix

• 令 $G = <V,E>,~|V| = n,,~|E| = e$，則準備一個 matrix $A:n * e$
  • 若 $e_k$ 邊為 $(i,j)$，則 $A[i, e_k] = A[j, e_k] = 1$，其餘為 0

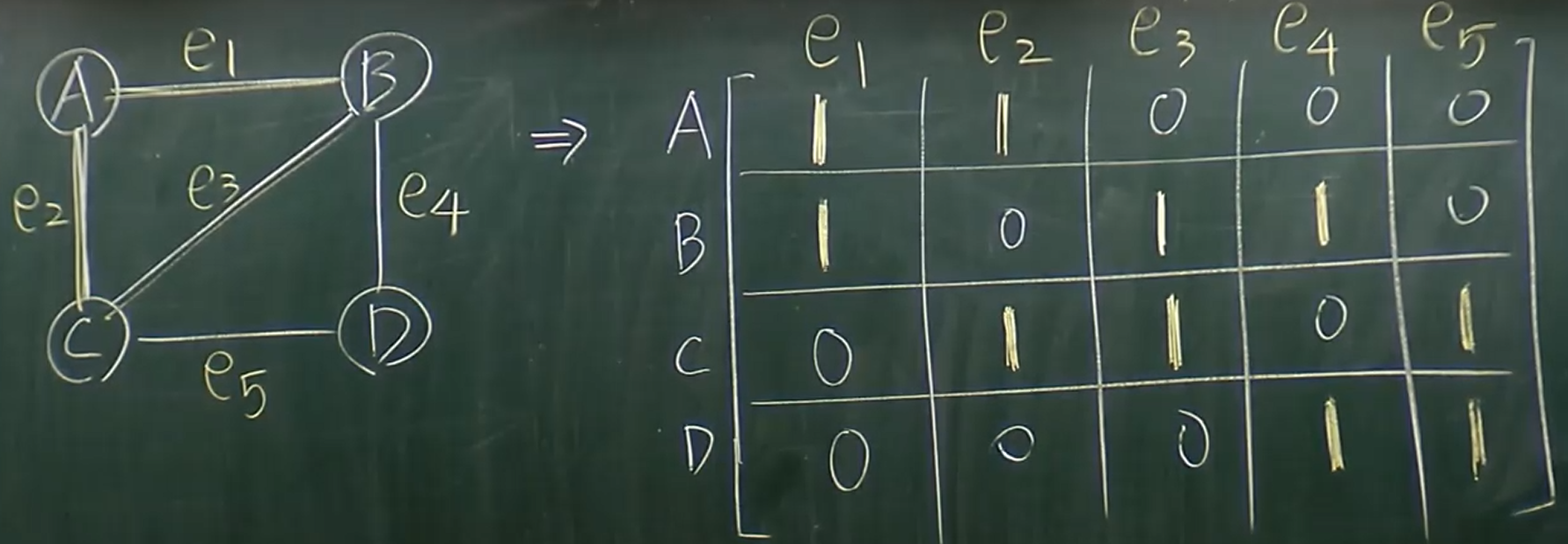
Graph Traversal

拜訪圖中每個頂點各一次

DFS

• 以無向圖為例

for i = 1 to n{
    visited[i] = false
}

DFS(v: start vertex){
    visited[v] = true
    for each vertex w adjacent to v{
        if(!visited(w)) DFS(w)
    }
}

• DFS order 並非唯一
  • 通常會規定依 vertex No. 小者優先走訪，如此 order 唯一

邊分類

• 當使用 DFS 進行有向圖的遍歷，可以將邊分為 4 類:
  • Tree edge: 遍歷追蹤時所經過的邊
    • 指向的 vertex 為還未遍歷過的 (white)
  • Back edge: 指向自己的祖先
    • 指向的 vertex 為已遍歷過，但尚未 DFS 完成 (gray)
  • Forward edge: 指向自己的後代
    • 指向的 vertex 為已遍歷過，且 DFS 完成 (black)
    • discovered time 比自身晚 (大)
  • Cross edge: 指向與自己無關的 vertex
    • 指向的 vertex 為已遍歷過，且 DFS 完成 (black)
    • discovered time 比自身早 (小)

• 遍歷順序為: $u \rightarrow v \rightarrow y \rightarrow x \rightarrow w \rightarrow z$

• 當使用 BFS 進行有向圖的遍歷，可以將邊分為 2 類:

  • Tree edge: 遍歷時所經過的邊
  • Back edge: 遍歷時沒有經過的邊
    • 如果指向的點為 parent (父親)，不為 Back edge

BFS

• 以無向圖為例

for i = 1 to n{
    visited[i] = false
}

BFS(v: start vertex){
    visited[v] = true
    queue Q
    Q.push(v)
    while(!Q.empty()){
        u = Q.front()
        Q.pop()
        for each vertex w adjacent to u{
            if(!visited(w)){
                visited[w] = true
                Q.push(w)
            }
        }
    }
}

• BFS order 並非唯一
  • 通常會規定依 vertex No. 小者優先走訪，如此 order 唯一

比較表

	DFS	BFS
資料結構	Stack	Queue
時間 (Adjacency Matrix)	$O(n^2)$	$O(n^2)$
時間 (Adjacency Lists)	$O(e)$ / $O(n+e)$	$O(e)$ / $O(n+e)$

• 對於二元樹而言
  • DFS: 類似 Preorder Traversal
  • BFS: 類似 Level-order Traversal

Spanning Tree (展開樹/生成樹)

• 給定一個 connected 無向圖 $G = <V,E>$，令 $S = <V,T>$ 是 $G$ 的一個 Spanning Tree，則 $S$ 滿足:
  • $E = T + B$
    • $E$ 為 Tree edge
    • $B$ 為 Back edge
  • 在 $S$ 中，任何頂點對之間，只存在一條 (unique) simple path
  • 若自 $B$ 中任取一邊加入 $S$ 中，必定會形成一個 (unique) cycle
• 若 $G$ 為 unconnected，則沒有 Spanning Tree
• 若 $G$ 為 connected，則 Spanning Tree$\geq 1$棵
• 若 $G$ 的頂點數為 $ n$，則其 Spanning Tree 的邊數必為 $n - 1$
• 一個 connected 無向圖 $G$ 的任意兩個 Spanning Tree (若存在) 必有共同邊?
  • False: 不一定
  • 反例: 4 個頂點的完全圖 (Z 字形連接)

Minimum Spanning Tree (最小生成樹)

• 給定一個 connected 無向圖 $G = <V,E>$，其邊上附有成本 (加權) 值，則在 $G$ 的所有 Spanning Tree 中具有最小的邊成本總和者
• 若圖中有多條邊具有相同成本，則 Minimum Spanning Tree$ 可能 \geq 1$棵
• 若圖中每條邊之成本皆不同 (unuque)，則 Minimum Spanning Tree 唯一
• 求 Spanning Tree 之演算法 (Greedy strategy):
  • Kruskal’s Algorithm
  • Prim’s Algorithm
  • Sollin’s Algorithm

Kruskal’s Algorithm

• 給定一個 connected 無向圖 $G = <V,E>$
• Steps:
  1. 自 $E$ 中挑出最小成本的邊 $(u,v)$
  2. 判斷 $(u,v)$ 加入 Spanning Tree $S$ 中是否會形成 cycle
     • 無 cycle: $(u,v)$ 加入 $S$ 中
     • 有 cycle: 放棄 $(u,v)$
  3. 重複 1.2. 直到挑出 $|V| - 1$ 條邊，或 $E$ 為空
  4. (可省) 若 $S$ 中邊數 $\leq |V| - 1$，則 $G$ 沒有 Spanning Tree
• 時間複雜度
  • 最多執行 $|E|$ 輪
    • Delete-min cost edge $(u,v)$ from $E$
    • 判斷 $(u,v)$ 加入 $S$ 是否造成 cycle
  • Delete-min 若使用 Heap 保存各邊成本，則需要 $O(\log{|E|})$
  • cycle 檢查利用 Disjoint Set 的 Union, Find 操作，約需要 $O(1)$
    • 假設採用 Union-by-Height, Find-with-path-Compression
    • 檢查 $Find(u)$ 與 $Find(v)$ 的值是否相同 (屬於相同 set 會造成 cycle)
    • $(u,v)$ 加入 $S$ 中: $Union(u,v)$
  • 總時間為 $|E| * (O(\log{|E|}) + O(1)) = O(|E|\log{|E|})$
    • $|E| < |V|^2 \Rightarrow O(|E|\log{|V|})$

Prim’s Algorithm

• 給定一個 connected 無向圖 $G = <V,E>, V = 1,2,3...,n$，令 $U = {1}$ (代表起始 vertex，可以隨意選擇)
• Steps:
  1. 挑出最小成本的邊 $(u,v)$，其中 $u \in U$ 且 $v \in V-U$
  2. $(u,v)$ 加入 $S$ 中，且將 $v$ 自 $V-U$ 中移入 $U$
  3. 重複 1.2. 直到 $U=V$
• 時間複雜度
  • use Adjacency Matrix: $O(|V|^2)$
  • use Heap: $O(|E|\log{|V|})$
  • use Fibonacci Heap: $O(|V|\log{|V| + E})$

Sollin’s Algorithm

• 一開始把每個頂點視為一個獨立的樹之 Root
• Steps:
  1. 從每棵樹中挑出最小成本之 Tree edge
  2. 刪除重複挑出的邊，只保留一份
  3. 重複 1.2. 直到只剩下一棵樹

最短路徑問題

	Dijkstra’s Algo	Bellmen-Ford Algo	Floyd-Warshall Algo
解決問題	單源最短路徑	單源最短路徑	全域最短路徑
策略	Greedy	DP	DP
Time	$O(V^2)$	$O(V^3)$	$O(V^3)$
圖是否可有負邊	不可	可	可
圖是否可有負 cycle	不可	不可	不可

Dijkstra’s Algorithm

• 給定一個 有向圖 $G = <V,E>,~|V| = n$,，其邊上附有cost (length) 值
• 使用的資料結構
  • Cost Matrix: 一個 $n * n$ 的 Matrix，其中 $Cost[i,j] =$
    • 邊成本值$,~if <i,j> \in E$
    • 邊成本值$,~if~i = j$
    • 邊成本值$,~if <i,j> \notin E$
  • $S:~[1,2,...,n]$ of Boolen，其中 $S[i]=$
    • False (0): 起點到 $i$ 點之最短路徑尚未確定
    • True (1): 起點到 $i$ 點之最短路徑已確定
    • 初值皆為 False
  • $Dist:~[1,2,...,n]$ of Int，其中 $Dist[i]=$
    • 起點到 $i$ 點之最短路徑長
    • 初值為 Cost Matrix 中起點那一列元素值
• Steps:
  1. 自尚未確定最短路徑的點 ($S[i] == 0$) 中，挑出 Dist 最小的點，令其為 $u$，並設定 $S[u] = 1$
  2. 對於 $u$ 的所有相鄰點 $w$，如果 $S[w] == 0 $，則檢查是否可以優化其 Dist (Relax) (經過 $u$ 到達 $w$ 距離更短)
  3. 重複 1.2. $n - 2$ 次
• 重要假設條件: 無負邊，否則可能無法求出正確值
• 可以額外建立一個 array 儲存各點之 parent，方便回推最短路徑
• 時間複雜度 [Algo]
  • use Heap: $O(|E|\log{|V|})$
  • use Fibonacci Heap: $O(|V|\log{|V| + E})$
  • 與 Prim's Algorithm 相同: Base on BFS concept

Bellmen-Ford Algorithm

• 給定一個 有向圖 $G = <V,E>,~|V| = n$,，其邊上附有cost (length) 值
• 定義: $Dist^K:~[1,2,...,n]$ of Int，其中 $Dist^K[i]=$
  • 起點到 $i$ 點之最短路徑長 且經過的邊數 $\leq K$
  • $Dist^1$ 為初值，數值為 Cost Matrix 中起點那一列元素值
• Steps:
  • 依序求出 $Dist^2,Dist^3...Dist^{n - 1}$，$Dist^{n - 1}$ 即為結果
    • 針對 $Dist^K[i]$，對每個指向 $i$ 的邊進行檢查是否能 Relax
• 時間複雜度
  • $O(|V|^3)$
  • $O(|V| * |E|)$ [Algo]
• 檢查是否有 負 cycle
  • 跑完正常的 Bellmen-Ford Algo (n - 1 輪)
  • 再跑一輪，如果有 $Dist^n[i]$ 可以 Relax，則存在 負 cycle

Floyd-Warshall Algorithm

• 給定一個 有向圖 $G = <V,E>, V = 1,2,3...,n$
• 定義: $A^K$: 一個 $n * n$ 的 Matrix，其中 $A^K[i,j]=$
  • $i$ 到 $j$ 之最短路徑長，且途中經過的頂點編號必須 $\leq K$
  • $A^0$ 為初值，同 Cost Matrix
• Steps:
  • 依序求出 $A^1,A^2...A^n$，$A^n$ 即為結果
    • 針對 $A^K[i,j]$，進行檢查是否能 Relax ($i\rightarrow j~or~i\rightarrow k\rightarrow j$)
• 時間複雜度
  • $O(|V|^3)$

$A^+,~A^*$ 矩陣

• 給定一個 有向圖 $G = <V,E>,~|V| = n$
• $A^+$ 矩陣: Transitive Closure Matrix
  • 一個 $n * n$ 的 Matrix，其中 $A^+[i,j]=$
    • $1,~if$ $i$ 到 $j$ 有 path，且長度 $\geq 1$
    • $0,~otherwise$
• $A^*$ 矩陣: Reflexive-Closure Matrix
  • 一個 $n * n$ 的 Matrix，其中 $A*+[i,j]=$
    • $1,~if$ $i$ 到 $j$ 有 path，且長度 $\geq 0$
    • $0,~otherwise$
• $A^* = A^+ \cup I$ (單位矩陣)

AOV Network & Topological sort

AOV (Activity On Vertex) Network

• 給定一個 有向圖 $G = <V,E>$，代表 AOV Network，其中:
  • Vertex: 代表工作 (Activity)
  • Edge: 代表工作執行之先後順序
    • $i \rightarrow j$ 存在代表 $i$ 必須先於 $j$ 執行
• 用於判斷計畫工作間的執行是否合理，即至少要有 $\geq 1$ 組合理的工作順序 (Topological sort)

Topological sort

• 給予一個不具 cycle 的 AOV Network，則至少可以產生 $\geq 1$ 組合理的頂點拜訪順序，滿足:
  • 在 AOV Network 中，若 $i$ 有 path 到達 $j$，則在此順序中， $i$ 必定出現在 $j$ 之前
• Steps:
  1. 找出 In-degree == 0 之 Vertex $i$
  2. 輸出 $i$ 且刪除從 $i$ 射出的邊
  3. 重複 1.2. 直到所有點都已經輸出，或是沒有 In-degree == 0 之 Vertex
     • 如果不是所有點皆已經輸出，則無 Topological sort (cycle 存在)
• Steps [Algo]: 進行 DFS，根據 Vertex Finish 的時間由後往前排序

AOE Network & critical path & critical task

AOE (Activity On Edge) Network

• 給定一個 有向圖 $G = <V,E>$，代表 AOE Network，其中:
  • Vertex: 代表事件 (Event)
  • Edge: 代表工作 (Activity)
  • Edge 上數字: 代表工作完工所需天數
• 意義:
  • 所有射入事件 Vertex 之工作皆完成後，事件才會發生
  • 事件發生後，從該 Vertex 射出之工作才可以開工
• 用於計畫之專案管理
• 求完成計畫之最短天數: critical path 之長度
  • start 到 end 之最長路徑長
  • critical path 可能有多條
  • critical task 上的所有工作
• 要加速哪些工作可以有效縮短計畫完工天數:
  • 所有 critical path 上的交集 (共同) 工作
• 哪些工作可以 delay，又可以 delay 多久不影響進度
  • 不在 critical path 上的工作皆可 delay
  • delay 時間:
    • 先求各事件之最早發生時間: start 到各點之最長路徑長
    • 再求各事件之最晚發生時間: 從 end 往回推各點
    • 求各工作之最早開工 (前一事件的最早發生時間)、最晚開工時間 (後一事件的最晚發生時間)，根據兩者之差距求得

Articulation Point

• 在一個 connected 無向圖 中，若刪除某頂點及其連結的邊，則剩下的圖變為 unconnected，該點稱之為 Articulation Point
• Biconnected Graph:
  • 一個不具有 Articulation Point 之 connected 無向圖
• Biconnected Component:
  • 給定一個 connected 無向圖 $G = <V,E>$，令 $G'$ 是 $G$ 的一個子圖，且滿足:
    • $G'$ 是 Biconnected Graph
    • $G'$ 是 Max Component (沒有其他 Biconnected Graph 子圖可包含 $G'$)
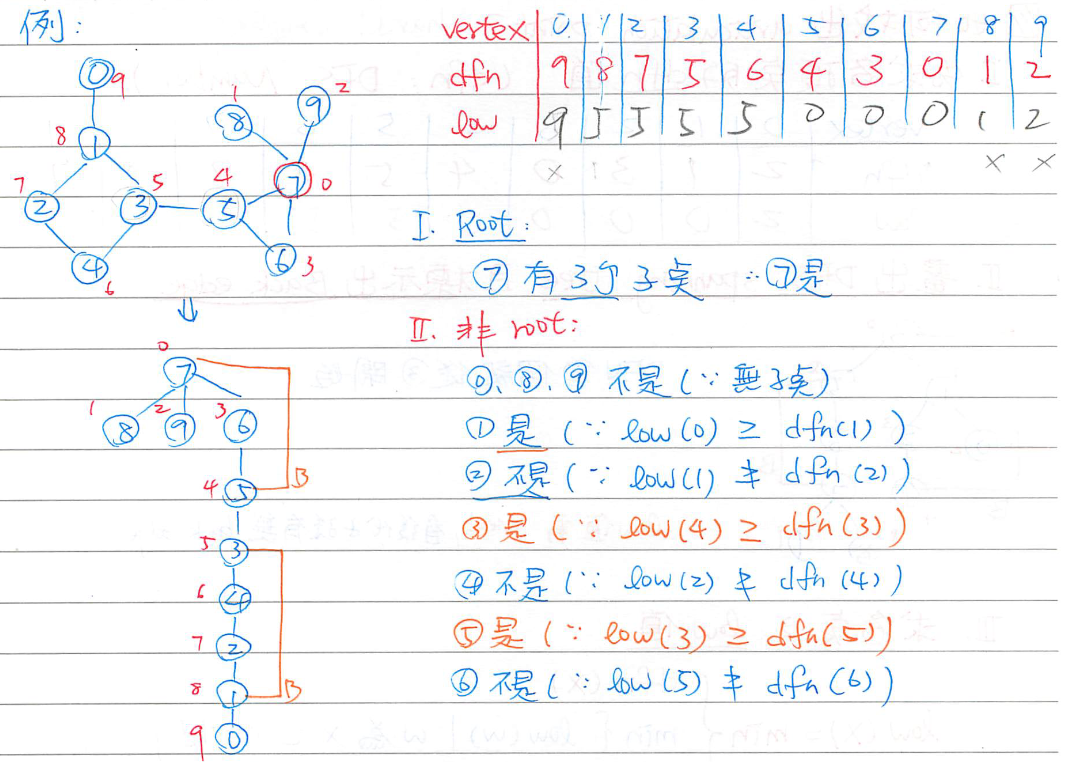
• 求 Articulation Point:
  • 從某點開始做 DFS，求各點之 dfn (DFS Number: 拜訪順序)
  • 畫出 DFS Spanning Tree 且標示出 Back edge
  • 求出各點之 low 值:
    • $low(x) = min(dfn(x), \{dfn(y)~|~y~為~x~的後代~(含~x)~中最多經過一條~Back~edge~所到之點\})$
  • 判斷規則:
    • 對於 root，若其有 $\geq 2$ 個子點，則為 Articulation Point，否則不是
    • 對於 非 root 頂點 $x$，令 $y$ 為 $x$ 之任一子點，若存在 $low(y) \geq dfn(x)$ 則 $x$ 為 Articulation Point