考研相關文章參考資料為 wjungle 大神提供的筆記
Array 元素之位置
一維陣列
- A:array[l...u] of items
- 共有 u−l+1 格
- 起始位置: l0
- 元素大小: d
- A[i] 的位置: l0+(i−l)∗d
二維陣列
- A:array[l1...u1,l2...u2] of items
- 有 u1−l1+1 列,u2−l2+1 行
Row-major
- A[i,j]=l0+[(i−l1)∗(u2−l2+1)+(j−l2)]∗d
Column-major
- A[i,j]=l0+[(j−l2)∗(u1−l1+1)+(i−l1)]∗d
N 維陣列
- A:array[l1...u1,l2...u2,l3...u3,...,ln...un] of items
- 令 km=um−lm+1(m=1,2,...,n)
Row-major (由左往右)
- A[i1,i2,...,in]=l0+[(i1−l1)∗k2∗k3∗...∗kn+(i2−l2)∗k3∗...∗kn+...+(in−1−ln−1)∗kn+(in−ln)]∗d
- =l0+{∑p=1n[(ip−lp)∗∏q=p+1nkq]}∗d
- 令 ∏q=n+1nkq=1
Column-major (由右往左)
- A[i1,i2,...,in]=l0+[(in−ln)∗kn−1∗kn−2∗...∗k1+(in−1−ln−1)∗kn−2∗...∗k1+...+(i2−l2)∗k1+(i1−l1)]∗d
- =l0+{∑p=1n[(ip−lp)∗∏q=1p−1kq]}∗d
- 令 ∏q=10kq=1
特殊矩陣
下三角矩陣
Lower-Triangular Matrix
- 令 A 為 n∗n 方陣,且對角線 (不含) 右上方均為 0 元素,其餘為元素
- A[i,j]=0, if i<j
- 元素個數: 2n(n+1)
- 為了節省空間,可用一個矩陣 B:array[1...2n(n+1)] 存放 A[i,j] 的元素,其中 B[k] 對應 i,j 的方式為:
Row-major
- k=2i(i−1)+j
Column-major
- k=n(j−1)−2j(j−1)+i
上三角矩陣
Upper-Triangular Matrix
- 令 A 為 n∗n 方陣,且對角線 (不含) 左下方均為 0 元素,其餘為元素
- A[i,j]=0, if i>j
- 元素個數: 2n(n+1)
- 為了節省空間,可用一個矩陣 B:array[1...2n(n+1)] 存放 A[i,j] 的元素,其中 B[k] 對應 i,j 的方式為:
Row-major
- k=n(i−1)−2i(i−1)+j
- 下三角之
Column-major 公式 i,j 對調
Column-major
- k=2j(j−1)+i
- 下三角之
Row-major 公式 i,j 對調
對稱矩陣
Symmetrix Matrix
- 令 A 為 n∗n 方陣,且 A[i,j]=A[j,i]
- 為了節省空間,可用一個矩陣 B:array[1...2n(n+1)] 存放下/上三角部分元素即可,其中 B[k] 對應 i,j 的
Single expression (單一公式) 為:
- k=2Max(i,j)(Max(i,j)−1)+Min(i,j)
帶狀/寬帶矩陣
Band Matrix
- 令 An,a,b 為 n∗n 方陣,且
- 對角線左下方 a 條斜線為元素
- 對角線右上方 b 條斜線為元素
- 其餘為 0 元素
- 元素個數: 2a(2n−a+1)+2b(2n−b+1)−n
Link list 種類
Circular link list
- 將
Single link list 的最後一個 Node 之 pointer 指回第一個 Node
- 不論從何點開始皆可拜訪所有 Nodes
- 回收整條串列空間 (加入
AV-list): O(1)
Double link list
- Linking 方向有兩個之 link list
LLink: 指向前一個 NodeRLink: 指向後一個 Node- 通常會加入
Head node (串列首): 不存資料
- 插入 Node: 需要改變 4 個 pointer
- 刪除 Node: 需要改變 2 個 pointer
比較表
| Single link list |
Double link list |
| 單向,只能知道前 or 後一個 Node |
雙向,同時知道前後一個 Node |
| 從頭開始才能遍歷,可靠性差 |
可從隨意位置遍歷,可靠性佳 |
| 插入、刪除 Node 簡單 |
插入、刪除 Node 複雜 |
| Linking 空間少 |
Linking 空間多 |
Link list 操作
- Length: 求串列長度
Single link list: O(n)Circular link list: O(1)
- Concatenate: 兩條
Circular link list 合併
- Invert: 反轉
Single link list
Generalize list
-
令 A=(a1,a2,...,an) 是一個 Generalize list, A 有 n 個元素 a1,a2,...,an,而 ai 元素的型態有兩種:
- Atomic data
- Sublist (另一個
Generalize list)
-
術語:
- ∣A∣: 表 A 之長度
Head of A: a1Tail of A: (a2,...,an)
-
資料結構:
| Tag |
變動欄位 |
Link |
| True |
Data (Atomic data) |
|
| False |
dlink (Pointer to Sublist) |
|
Generalize list 操作
- Copy a list
- Equal: 判斷相等
- Depth
- 定義為所有
Sublist 之 Depth 最大值 + 1 (Nil: 0)
多項式表示
Array
- 根據
指數由高至低儲存其係數,假設最高項指數為 n,則準備 A:array[1,2...,n+2] of int
- 第一位儲存 n 的數值
- 之後依序儲存各項係數
- 缺點: 對於最高項指數很大,但零項次很多的多項式,會浪費空間
- 只儲存
非零項次的指數與係數,假設多項式有 k 個非零項次,則準備 A:array[1,2...,2k+1] of int
- 第一位儲存 k 的數值
- 之後依序儲存各項指數及係數
- 缺點: 不適用於零項次很少的多項式 (需要空間約為 1. 的兩倍)
Link list
-
使用 Link list 儲存指數與係數
- 資料結構: exp (指數) | coe (係數) | link
- 擴展 (多變數): x-exp | y-exp | coe | link
- 缺點: 可能導致各個 Node 資料結構不一致 (變數數量不同)
-
使用 Generalize list 儲存資料
| Tripple |
變動欄位 |
exp |
link |
| Var |
Variable (存變數名稱) |
空 |
|
| Ptr |
dlink (Pointer to Sublist) |
|
|
| No. |
coe (係數值) |
|
|

Sparse Matrix 表示
稀疏矩陣: 含有大量 0 元素的 m∗n 矩陣
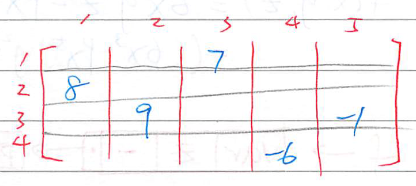
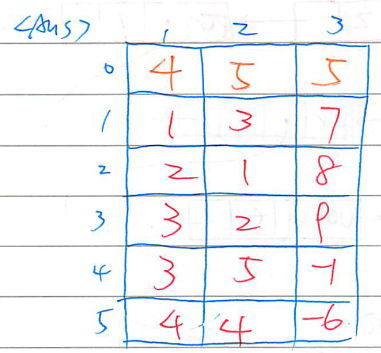
Array
- 直接用 m∗n 矩陣存放
- 只存非零元素之資訊,以
<Row, Col, Value> 的結構儲存資料
- 假設一個 m∗n
Sparse Matrix 含有 k 個非零元素,則以 A:array[0...k,1...3] of int 表示
- 第 0 列儲存
matrix 資訊: <m, n, k>
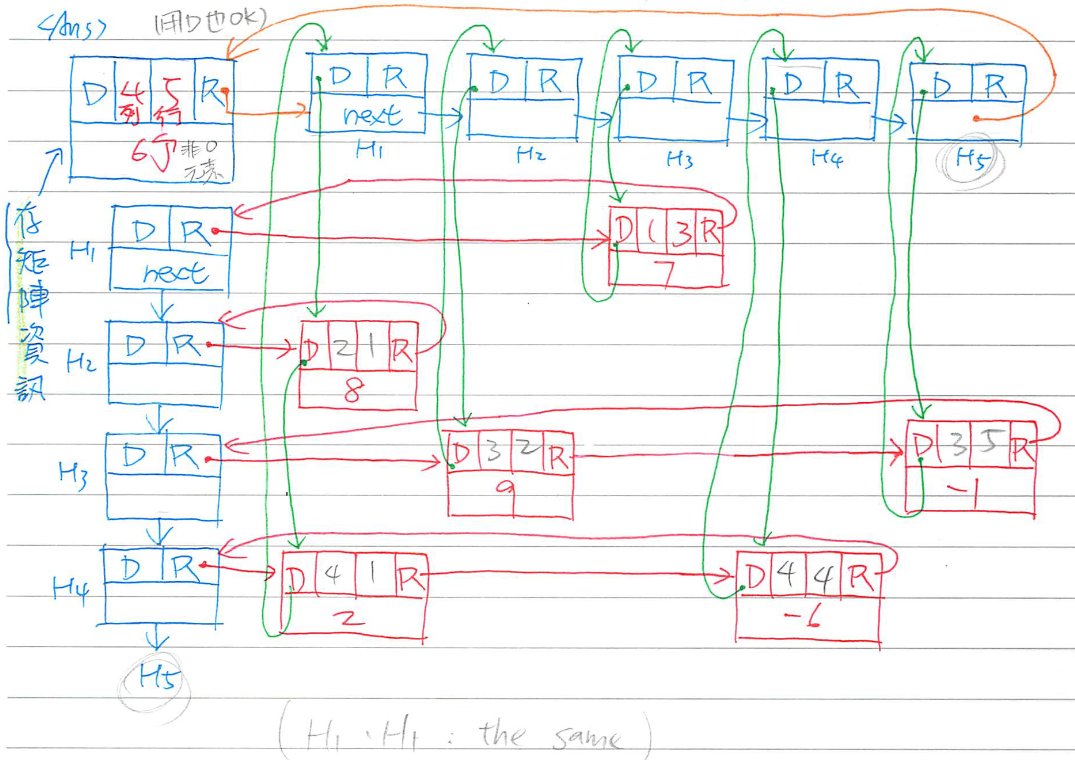
Link list
- 使用
Double link list: 儲存 Row 及 Col 方向,且 Node 分為兩類:
Head node: 串列首,不存資料
- 資料結構: Head (True) | Down | Right |
Next
- Down: pointer 指向所在行的第一個元素
- Right: pointer 指向所在列的第一個元素
- Next: pointer 指向下一個
Head node
Head node 數量 = Max(列數,行數)
Element node
- 資料結構: Head (False) | Down | Right |
Row | Col | Value
- Down: pointer 指向下一個行元素
- Right: pointer 指向下一個列元素
- Row, Col, Value: 非零元素之資料